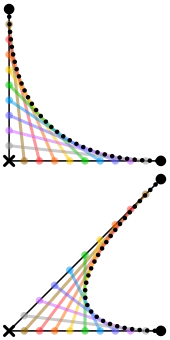Search
↩️

Ch.7 Beziers Curves

course
last review
2023/09/19
mastery
ranger
progress
not started
date
2023/09/19
4 more properties
Previous chapter
Ch.5 Curves

Today’s MAIN QUEST

Bezier Curve를 알아보고, Application과 Problem에 대해 이해한다.

Bezier Curves란?

C2 Continuity를 만족하기 위해 고안해낸 곡선
기본적으로 Approximation Curve. 모든 점을 근사하는 가장 가까운 곡선을 그려낸다.

Linear Bezier Curves

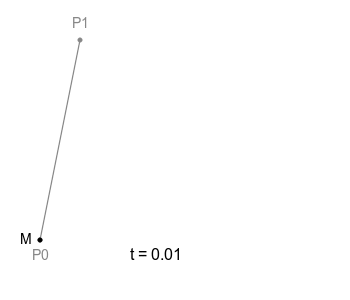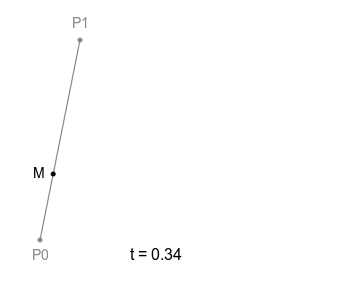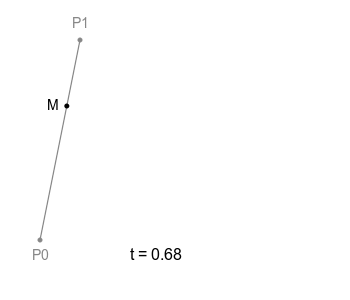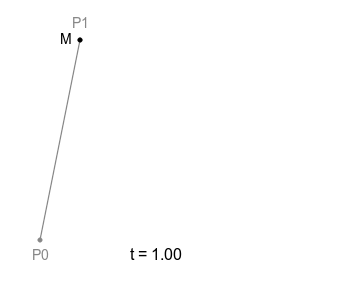
어떤 선분 P0 P1이 있다고 가정하자. 그 선분 위를 움직이는 점 M이 있다고 할 때 다음과 같이 움직일 것이다. 점 M의 이동경로가 곧 베지에 곡선임을 기억하자.
1차 베지에 곡선
M의 위치는 다음과 같다.
vM=vP0×(1−t)+vP1×tv_M = v_{P_0}\times (1-t) + v_{P_1}\times t
단순한 InterPolation과 다를 것 없다.

Quadratic Bezier Curves

2차 베지에 곡선
여기에서 선분 P1P2를 추가해보자.
각 선분별로 그 위를 움직이는 점 M0 M1이 있을 것이며 각 점의 좌표는 다음과 같다.
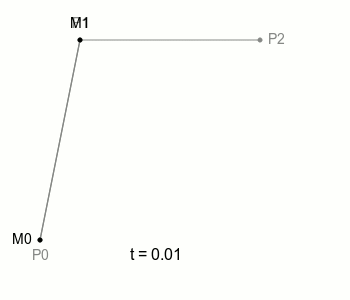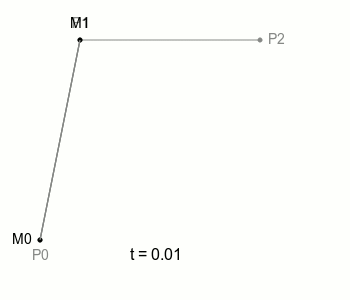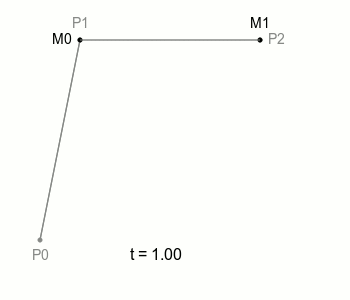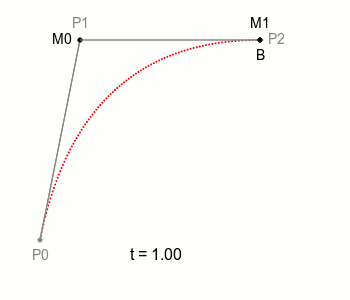
vM0=vP0×(1−t)+vP1×tvM1=vP1×(1−t)+vP2×tv_{M_0} = v_{P_0}\times (1-t) + v_{P_1}\times t \\ v_{M_1} = v_{P_1}\times (1-t) + v_{P_2}\times t
이때 각 점 M0와 M1을 똑같이 t에 비례하여 움직이는 점 B가 있다면 어떨까? 이 2차 점 B가 바로 2차 베지어 곡선이 된다.
vB=vM0×(1−t)+vM1×tv_B = v_{M_0}\times (1-t) + v_{M_1}\times t
이를 원래 입력 값이었던 점 P0 P1 P2에 대한 식으로 풀어보자.
vB=vM0×(1−t)+vM1×tvB=(vP0×(1−t)+vP1×t)×(1−t)+(vP1×(1−t)+vP2×t)×tvB=(vP0−tvP0+tvP1)−t(vP0−tvP0+tvP1)+t(vP1−tvP1+tvP2)v_B = v_{M_0}\times (1-t) + v_{M_1}\times t \\ v_B = (v_{P_0}\times (1-t) + v_{P_1}\times t)\times (1-t) + (v_{P_1}\times (1-t) + v_{P_2}\times t)\times t \\ v_B = (v_{P_0}-tv_{P_0}+tv_{P_1})-t(v_{P_0}-tv_{P_0}+tv_{P_1})+t(v_{P_1}-tv_{P_1}+tv_{P_2})\\
vB=vP0+2t(vP1−vP0)+t2(vP0−2vP1+vP2)v_B=v_{P_0} + 2t(v_{P_1}-v_{P_0}) + t^2(v_{P_0}-2v_{P_1}+v_{P_2})
vB=(1−2t+t2)vP0+2(1−t)tvP1+t2vP2v_B = (1-2t+t^2)v_{P_0}+2(1-t)tv_{P_1}+t^2v_{P_2}

Cubic Bezier Curves

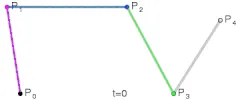
마지막으로 3번째 선분이다.
식은 다음과 같다.
vM0=vP0×(1−t)+vP1×tvM1=vP1×(1−t)+vP2×tvM2=vP2×(1−t)+vP3×tv_{M_0} = v_{P_0}\times (1-t) + v_{P_1}\times t \\ v_{M_1} = v_{P_1}\times (1-t) + v_{P_2}\times t \\ v_{M_2} = v_{P_2}\times (1-t) + v_{P_3}\times t
vB0=vM0×(1−t)+vM1×tvB1=vM1×(1−t)+vM2×tv_{B_0} = v_{M_0}\times (1-t) + v_{M_1}\times t \\ v_{B_1} = v_{M_1}\times (1-t) + v_{M_2}\times t
vB=vB0×(1−t)+vB1×tv_{B} = v_{B_0}\times (1-t) + v_{B_1}\times t
이제 점 B를 각 점으로만 나타내보자.
vB=vM0+2t(vM1−vM0)+t2(vM0−2vM1+vM2)=(vP0×(1−t)+vP1×t)+2t((vP1×(1−t)+vP2×t)−(vP0×(1−t)+vP1×t))+t2((vP0×(1−t)+vP1×t)−2(vP1×(1−t)+vP2×t)+(vP2×(1−t)+vP3×t))v_B=v_{M_0} + 2t(v_{M_1}-v_{M_0}) + t^2(v_{M_0}-2v_{M_1}+v_{M_2})\\ =(v_{P_0}\times (1-t) + v_{P_1}\times t)\\+2t((v_{P_1}\times (1-t) + v_{P_2}\times t)-(v_{P_0}\times (1-t) + v_{P_1}\times t))\\+t^2((v_{P_0}\times (1-t) + v_{P_1}\times t)-2(v_{P_1}\times (1-t) + v_{P_2}\times t)+(v_{P_2}\times (1-t) + v_{P_3}\times t))
vB=(1−t)3vP0+(1−t)2tvP1+(1−t)t2vP2+t3vP3v_B = (1-t)^3v_{P_0}+(1-t)^2tv_{P_1}+(1-t)t^2v_{P_2}+t^3v_{P_3}
어후 길다.
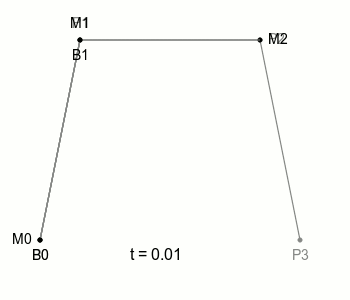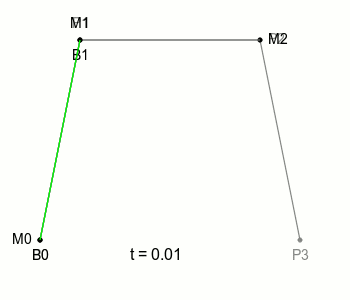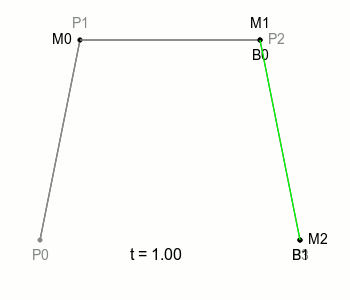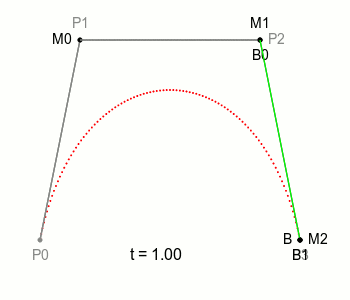
이런 식으로 4, 5차 그 이상까지 전개할 수 있으며 이 최종 점 VBV_B가 이동하는 궤적이 베지어 곡선의 형태이다.
그런데 각 점에 대해서 전개 해놓은 상태를 봤을 때 이를 일반화 할 수 있을 것 같다.

Math Generalization

각 차수에 대한 베지어 곡선을 다시 꺼내보자.
Linear Bezier Curves
vM=vP0×(1−t)+vP1×tv_M = v_{P_0}\times (1-t) + v_{P_1}\times t
Quadratic Bezier Curves
vB=(1−2t+t2)vP0+2(1−t)tvP1+t2vP2v_B = (1-2t+t^2)v_{P_0}+2(1-t)tv_{P_1}+t^2v_{P_2}
Cubic Bezier Curves
vB=(1−t)3vP0+(1−t)2tvP1+(1−t)t2vP2+t3vP3v_B = (1-t)^3v_{P_0}+(1-t)^2tv_{P_1}+(1-t)t^2v_{P_2}+t^3v_{P_3}
보이는가?
조절점이 n+1개일 때, 각 점VPnV_{P_n}에 대한 계수 t는 다음과 같이 일반화 할 수 있을 것이다.
VB(n+1)=∑k=0nC(n,k)⋅tk⋅(1−t)n−k⋅VPkV_B(n+1)=\sum^{n}_{k=0} C(n,k)\sdot t^k\sdot(1-t)^{n-k}\sdot V_{P_k}
깔끔하다. 이제 귀찮게 재귀함수를 써서 콜 스택을 할당하지 않고 베지어 곡선을 만들 수 있을 것이다.
…
혹은 재귀함수를 DP 타입 문제로 고칠수도 있다. 자세한 건 뒤에 나온다.

Features

1.
조절점이 항상 곡선 위에 있는 건 아니다. 오히려 조절점은 웬만한 곡선에서는 양 끝 지점에만 존재하는 경우가 많다.
2.
곡선의 차수는 조절점의 개수에서 1을 뺀 값이다. 조절점이 두 개일 땐 직선, 세 개일 땐 2차 곡선, 네 개일 땐 3차 곡선이 된다.
3.
곡선은 항상 조절점의 컨벡스 헐(convex hull, 볼록 껍질)안에 있다. 하단 참조

Convex Hull

베지어 곡선이 만들어지는 방식에 대해 생각해보자.
2차 베지어 곡선을 예시로 생각해보자.
1.
각 선분에 대한 내분점을 먼저 찍는다. 이 내분점은 선분을 벗어날 수 없다.
2.
내분점을 이어주는 새로운 선분을 만든다. 이 선분들은 반드시 삼각형 안에 존재한다.
3.
새로운 선분의 내분점은 반드시 삼각형 안에 존재한다.
따라서 베지어 곡선은 점 P0 P1 P2로 만든 Convex Hull(=삼각형)의 안에서만 성립할 수 있다.
수학적으로 검증해보자.
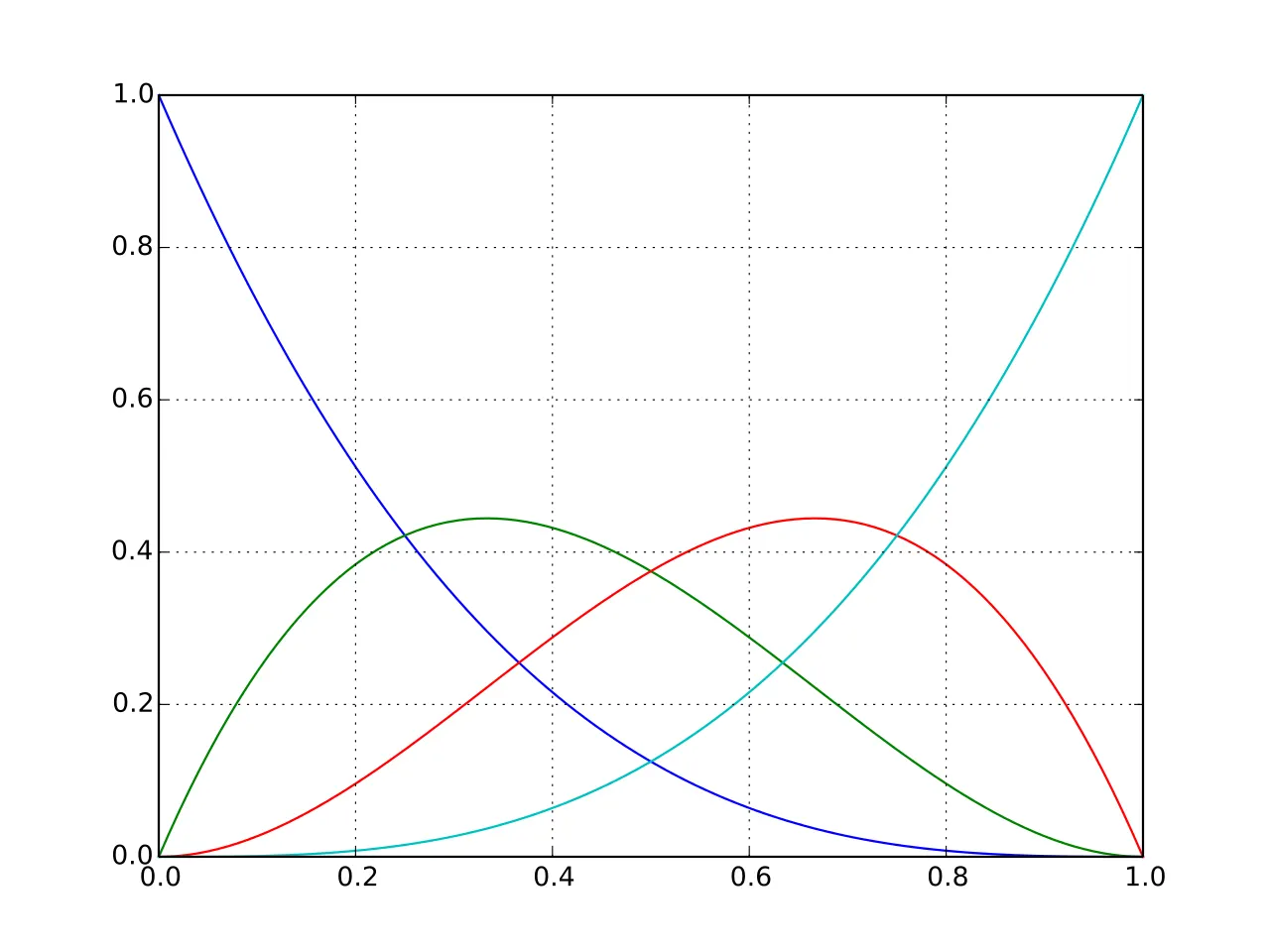
각 정점이 베지에 곡선에게 얼마나 영향을 주는지 알아보기 위해 다음과 같이 정의해보자.
VB(n+1)=∑k=0nBk,n(t)⋅VPkBk,n(t)=C(n,k)⋅tk⋅(1−t)n−kV_B(n+1)=\sum^{n}_{k=0} B_{k,n}(t)\sdot V_{P_k}\\ B_{k,n}(t) = C(n,k)\sdot t^k\sdot(1-t)^{n-k}
이때, Bk,n(t)B_{k,n}(t)는 t의 값에 따라 위와 같이 비율이 할당된다고 생각해도 괜찮을 것이다(수학적인 의미로 볼 때는 엄청 틀린 이야기지만)
특이한 점은 베지어 곡선이 해당 값을 모두 더했을 때 언제나 1을 유지한다는 성질을 가진다는 것이다. 자세한 건 여기 참조.
아핀 조합을 활용하여 Convex Hull과의 특성을 연관지을 수 있다.
이를 활용하여 교차 검사 최적화 라는 것이 가능하다.

De Casteljau Algorithm

Advanced

Closed Curve
Weighted Curve
Connected Curve

Problems

c1, c2 Coninuity를 모두 만족해야하므로 컨트롤할 수 있는 컨트롤 포인트의 개수가 줄어든다.

Q&A

앞선 Convex Hull Property에서 Convex Hull은 컨트롤 포인트를 모두 포함하는 임의의 Convex Hull, 즉 베지에 곡선은 이 임의의 Convex Hull을 만족하는 것인가?
Drawing Algorithm에서 y값이 급격하게 변하는 경우?
De Casteljau’s Algoritm과 수식의 Combination값을 DP로 만드는 것과 시간복잡도가 비슷한 것 같은데?
De Casteljau와 수학적 수식 둘 중에 어떤게 먼저 생긴건가? De Casteljau 방식을 노리고 수식을 만든건지 수식을 만들었는데 De Casteljau로 정리가 가능했던건지
C1 Continuity에 상수 k가 필요한가

References

중학생도 알 수 있는 베지에 곡선
중학생도 알 수 있는 베지에 곡선(Bezier Curves)
이 문서는 일본어 문서 「中学生でもわかるベジェ曲線」을 번역한 것으로 곡선을 그리거나 애니메이션 처리에 근간이 되는 베지에 곡선(Bezier Curves)의 원리에 관해서 쉽고 간단하게 소개합니다.
https://blog.coderifleman.com/2016/12/30/bezier-curves/
[원본문서]
中学生でもわかるベジェ曲線
ベジェ曲線をレンダリングしていたら面白くて丁寧に描いてしまった。せっかくなのでこれを使って誰にでもわかるように（たぶん中学生でも分かるように）ベジェ曲線というものが何かを説明してみたいと思う。 ベジェ曲線というのはなめらかな曲線を描くためのものなのだけど、説明はまず単なる直線...
http://blog.sigbus.info/2011/10/bezier.html
Bezier Curve - Wikipedia
Bézier curve
A Bézier curve (/ˈbɛz.i.eɪ/ BEH-zee-ay)[1] is a parametric curve used in computer graphics and related fields.[2] A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approximate a real-world shape that otherwise has no mathematical representation or whose representation is unknown or too complicated. The Bézier curve is named after French engineer Pierre Bézier (1910–1999), who used it in the 1960s for designing curves for the bodywork of Renault cars.[3] Other uses include the design of computer fonts and animation.[3] Bézier curves can be combined to form a Bézier spline, or generalized to higher dimensions to form Bézier surfaces.[3] The Bézier triangle is a special case of the latter.
https://en.wikipedia.org/wiki/Bézier_curve
De Casteljau’s Algorithm (DP?)
De Casteljau's algorithm
In the mathematical field of numerical analysis, De Casteljau's algorithm is a recursive method to evaluate polynomials in Bernstein form or Bézier curves, named after its inventor Paul de Casteljau. De Casteljau's algorithm can also be used to split a single Bézier curve into two Bézier curves at an arbitrary parameter value.
https://en.wikipedia.org/wiki/De_Casteljau's_algorithm
베지어 곡선
베지어 곡선
베지어 곡선(Bezier Curve)은 컴퓨터 그래픽스에서 사용되는 특별한 형태의 곡선으로, CSS 애니메이션 등에서 도형을 그릴 때 사용합니다.
https://ko.javascript.info/bezier-curve
Intersection Test Optimization
Next chapter
Ch.9 B-Spline Curves