2 : Geometric Objects

2024 HiTECH LABO STOVE LEAGUE
/study schedule
/
2 : Geometric Objects
Search
Share
💾
2 : Geometric Objects
course
last review
mastery
ranger
progress
done
date
2023/03/14
4 more properties
Previous chapter
Main QUEST
Introduction
Graphic Primitives
Point & Vector
Attributes of Vectors
Coordinate-Free Geometry
The Mathematical View : Affine Spaces
The relation between Vector Space and Affine Space
The Computer Science View : ADT(Abstract Data Type)
Affine Combination & Line
Combination of Affine Combination
a = 1인 경우
a = 0인 경우
a = 0.5인경우
Plane
Normal Vector
Summary
Coordinate Systems for Rendering
The Problem of Screen Coordinate System
OpenGL Normalized Coordinate Systems
Rendering Points
Remaining Questions
Rendering Lines
Naive Solution
A bit better algorithm : Line equation
Digital Differential Analyzer : DDA
ANOTHER Line Equation
Flood Fill : BFS Maze Problem
2023/03/16 - 폴리곤 렌더링 : Flood Fill 부터 다시 정리해야함.
Main QUEST
무엇을 그릴 것인가?
Q1 : 그려야 하는 것은 Shape[형상]인데, 어떻게 표현할 것인가?
Q2 : 이렇게 표현된 Shape를 래스터 디바이스로 어떻게 그릴 것인가? 
→ 픽셀을 어떻게 만드는가?
Introduction
렌더링이란 계산 가능한 모델을 픽셀로 바꾸는 방법
그리고자 하는 대상의 무엇을 알아야 할까?
•
모양 : Shapes
•
위치 : Locations
•
모습 : Appearances
•
질감 : Textures
등등…
이 중 Shapes에 대해서 자세하게 알아보자.
Graphic Primitives
우리가 표현하고자 하는 공간을 모두 분해했을 때 남는 가장 기초적인 요소
→ 정점(Vertex)
Shape를 표현하는 수학적 모델(Computational Model)
Point & Vector
•
위치
점이 가진 유일한 성질은 점의 위치. 수학적 점은 크기나 형상을 가지지 않는다.
점을 표현할 때 필요한 Attributes는 Position 뿐이다.
다만, 점과 점 사이의 관계를 나타내기 위해서는 Vector가 필요하다.
•
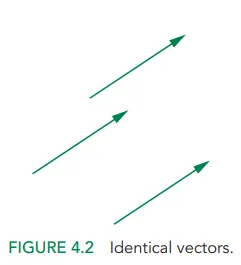
Vector는 공간 내에서 고정된 위치를 갖지 않는다.
세 벡터는 모두 같은 벡터이다.
따라서 그래픽스에서는 Position와 Vector를 표현해서 점들간의 관계를 나타낸다.
•
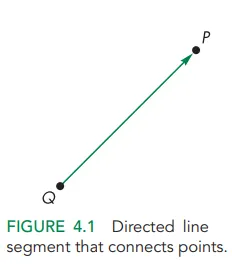
두 점은 방향성 선분directed line segment으로 연결한다.
Attributes of Vectors
•
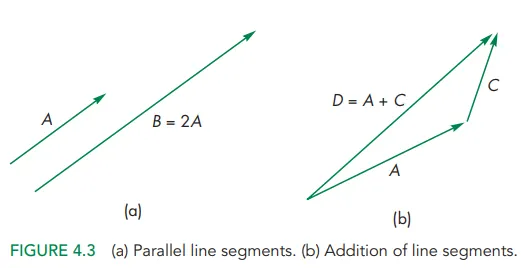
수미연결규칙(head-to tail rule)
◦
벡터 A의 헤드를 벡터C의 테일에 연결해 새로운 벡터 D가 생성이 가능하다.
•
스칼라 곱
◦
같은 방향이지만 B의 길이가 A의 2배이므로, B=2AB = 2AB=2A부불
의외로 Point가 할 수 없는 것
•
두 점을 이용해서 새로운 점을 구하는 연산
•
점x스칼라 → 새로운 점을 구하는 연산
⇒새로운 포지션의 점을 구하기 위해서는 점 + 벡터 연산이 필요하다!
이 연산을 점-벡터 덧셈이라고 하며, Output은 새로운 점이다.
P=Q + vP = Q\space + \space vP=Q + v
다른 관점에서 보면 (New)Point = (Previous)Point + (New)Vector 이므로,
v=P−Qv = P - Qv=P−Q
벡터는 두 점의 뺄셈으로 나타낼 수 있다.
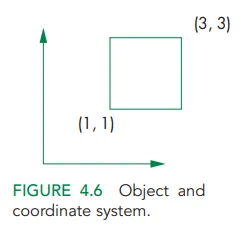
Coordinate-Free Geometry
점은 좌표계와 상관없이 공간상에 존재한다. 점을 정의하기 위해 좌표계가 필요한 것이 아니다!
좌표축을 제거했을때, 점이 더이상 어디에 있는지 명시적으로 지정할 수 없음.
임의의 위치와 방향을 갖는 좌표축에 상대적으로 지정된 것이며, 도형의 기하학적 정의를 설명하는데 아무런 영향을 주지 않음.
중요한 건, 근본적인 기하학적 관계는 유지된다는 점이다.
정사각형은 여전히 선분끼리 직교하며, 점들간의 거리도 같다.
The Mathematical View : Affine Spaces
앞서 점과 벡터와의 관계를 다음과 같이 나타냈었다.
A×V→A, (a,v)→a+vA \times V \rightarrow A, \space(a,v) \rightarrow a+vA×V→A, (a,v)→a+v
a가 점이라면 v에 의해 운반되는데, 운반된 결과는 다시 점이 되는 것이 아핀 변환에서의 벡터와 점의 관계이다.
1.
점 P에 영벡터를 더하면 점 P가 된다. 점에 아무런 힘도 안 가해진다면, 점은 움직이지 않는다.
a.
P+0⃗→PP+\vec0 \rightarrow PP+0→P
2.
아핀공간은 결합법칙이 성립된다.
a.
(a+v)+w=a+(v+w)(a+v)+w = a +(v+w)(a+v)+w=a+(v+w)
3.
v→a+v is bijectionv \rightarrow a + v \space is \space bijectionv→a+v is bijection
a.
bijection이란 두 집합에서 각 원소들이 정확히 1:1로 짝으로 매칭되는 것을 의미한다.
b.
바꾸어 말하면 점 a에 어떤 벡터를 더한 결과로 점 b가 나왔다는데 이를 만족하는 벡터 v는 단 하나만 존재한다는 것을 의미한다.
c.
벡터는 선형성을 가지므로 그 벡터의 정체는 아래 그림과 같이 점간의 최단 거리가 된다.
The relation between Vector Space and Affine Space
아핀 공간에서의 점이란 벡터 공간의 원점을 의미한다고 생각한다.
-이득우—
벡터를 원점에서 뻗어나가는 화살표로 표시함. → 벡터란 원점(Origin)에 있는 어떤 물체를 움직이는 무형의 힘인 것이다.
이동 변환을 구현하기 전까지 모든 벡터 공간은 원점을 기준으로 변했기 때문에 점의 개념에 큰 의미를 둘 필요가 없었다. 그러나 이동변환이 등장하며 원점에 대한 새로운 정의가 필요하게 되었다.
이동변환의 결과로 만들어지는 벡터공간은 (0,0)이 아닌 (x,y)위치에서 시작하는 새로운 공간이다.
그렇기 때문에 이동 변환으로 생기는 새로운 벡터 공간의 원점을 아핀 공간에서는 점이라고 하는 것이다.
즉, 아핀 공간에서는 원점이 없으므로 점과 점을 더할 수 없다.
The Computer Science View : ADT(Abstract Data Type)
수학적인 관점에서 Scalar, Point, Vector는 공리에 따라 결합되는 집합의 원소로 간주되어왔으나, 컴퓨터과학의 측면에서는 추상자료형으로 보는 것을 선호한다.
ADT는 데이터에 대한 연산들의 집합이다. 이 연산은 데이터가 내부적으로 어떻게 표현되고  구현되는지 독립적으로 정의된다.
vector u, v;
point p, q;
scalar a,b;
C++
복사
Affine Combination & Line
앞서 아핀공간에서 점과 점은 더해서 사용할 수 없다고 설명했다.
그런데 점과 점을 그대로 더하지 않고 선형 결합의 형태로 점에 스칼라 계수를 곱해 더한다면 특정 조건에서 새로운 점을 생성하는 것이 가능해진다.
2차원 평면상의 임의의 두 점 P1(x1,y1,1)P_1(x_1,y_1,1)P1​(x1​,y1​,1)과 P2(x2,y2,1)P_2(x_2,y_2,1)P2​(x2​,y2​,1)에 각각 스칼라 a,b를 곱한 선형 결합식은 다음과 같다.
a⋅P1+b⋅P2=(ax1+bx2,ay1+by2,a+b)a \cdot P_1 + b \cdot P_2 = (ax_1 + bx_2,ay_1+by_2, a+b)a⋅P1​+b⋅P2​=(ax1​+bx2​,ay1​+by2​,a+b)
이때 a+b가 1이 된다면, 점과 점을 결합해 새로운 점을 만들 수 있다!!
동일한 원리로 세 점에 대해서도 다음 수식과 같이 모든 스칼라의 sum이 1이면 점의 생성이 가능하다.
a⋅P1+b⋅P2+c⋅P3=P4(ax1+bx2+cx3, ay1+by2+cy3, a+b+c)a \cdot P_1 + b \cdot P_2 + c \cdot P_3 = P_4(ax_1 + bx_2 + cx_3,\space ay_1+by_2+cy_3,\space  a+b+c)a⋅P1​+b⋅P2​+c⋅P3​=P4​(ax1​+bx2​+cx3​, ay1​+by2​+cy3​, a+b+c)
여러 개의 점을 결합해 새로운 점을 생성하는 수식을 Affine combination이라고 한다.
각 점PiP_iPi​와 각 점에 대응되는 스칼라 값 cic_ici​에 대해 다음과 같이 간략화하며 마친다.
∑i=1nci⋅Pi  (s.t. ∑inci=1)\sum^{n}_{i=1}{c_i \cdot P_i} \space\space(s.t.\space \sum^n_ic_i=1)i=1∑n​ci​⋅Pi​  (s.t. i∑n​ci​=1)
참고로 위 식으로 인해 나타나는 영역을 Convex Hull이라고 한다.
Combination of Affine Combination
아핀 공간의 두 점에 대응되는 스칼라 값 a,b에 대해
a+b=1a+b=1a+b=1
을 만족해야 했는데, 이를 바탕으로 다음과 같이 정의하게 된다면 언제나 점의 생성을 보장받을 수 있다.
a⋅P1+(1−a)⋅P2=P′a\cdot P_1 + (1-a)\cdot P_2 = P'a⋅P1​+(1−a)⋅P2​=P′
a = 1인 경우
1⋅P1+0⋅P2=P′1 \cdot P_1 + 0\cdot P_2 = P'1⋅P1​+0⋅P2​=P′
a = 0인 경우
0⋅P1+1⋅P2=P′0\cdot P_1 + 1\cdot P_2 = P'0⋅P1​+1⋅P2​=P′
a = 0.5인경우
12⋅(x1,y1,1)+12⋅(x2,y2,1)=(x1+x22,y1+y22,1)\cfrac{1}{2}\cdot(x_1,y_1,1)+\cfrac{1}{2}\cdot(x_2,y_2,1) = (\cfrac{x_1+x_2}{2},\cfrac{y_1+y_2}{2},1)21​⋅(x1​,y1​,1)+21​⋅(x2​,y2​,1)=(2x1​+x2​​,2y1​+y2​​,1)
P1와 PO2의 중점이 만들어진다.
즉, P의 아핀결합으로 생성되는 점을 모두 모으면 P1,P2를 지나는 무한한 긴 선이 만들어진다.
즉 미지수 x에 대한 직선의 방정식 L(x)는 다음과 같이 표현될 수 있다.
L(x)=x⋅P+(1−x)QL(x) = x\cdot P+(1-x)QL(x)=x⋅P+(1−x)Q
Plane
아핀 공간에서 평면은 매개변수형 직선을 확장하여 정의가능하다.
세 점 P, Q, R이 있다고 가정하자.
P와 Q를 잇는 선분은 다음과 같다.
S(α)=αP+(1−α)Q  (0≤α≤1)S(\alpha) = \alpha P+(1-\alpha)Q \space \space(0\leq \alpha \leq  1)S(α)=αP+(1−α)Q  (0≤α≤1)
선분 위의 점 S를 선택하고, R에서 S까지의 선분을 형성해보자.
T(β)=βS+(1−β)R  (0≤β≤1)T(\beta) = \beta S+(1-\beta)R \space \space(0\leq \beta \leq  1)T(β)=βS+(1−β)R  (0≤β≤1)
이 점들은 α,β\alpha,\betaα,β에 의해 결정되며, P,Q,R에 의해 결정되는 평면을 형성한다.
T(α,β)=β[αP+(1−α)Q]+(1−β)RT(\alpha,\beta)=\beta[\alpha P + (1-\alpha)Q] + (1-\beta)RT(α,β)=β[αP+(1−α)Q]+(1−β)R
Q−PQ-PQ−P와 R−PR-PR−P는 벡터이며, 평면이 한 점과 평행하지 않은 두 벡터로부터 결정되는 것을 보였으므로 다음과 같이 P0,u,vP_0,u,vP0​,u,v에 의해 결정되는 평면의 식을 쓸 수 있다.
T(a,b)=P0+αu+βvT(a,b)=P_0+\alpha u + \beta vT(a,b)=P0​+αu+βv
 
•
Q−PQ-PQ−P와 R−PR-PR−P는 각각 u,vu,vu,v에 대응되므로, P0=PP_0 = PP0​=P가 자연스레 된다.
T(α,β)=βαP+β(1−α)Q+(1−β)RT(\alpha,\beta)=\beta\alpha P + \beta(1-\alpha)Q + (1-\beta)RT(α,β)=βαP+β(1−α)Q+(1−β)R
이때 α′=βα,β′=β(1−α),γ′=(1−β)\alpha' = \beta\alpha,\beta'=\beta(1-\alpha),\gamma'=(1-\beta)α′=βα,β′=β(1−α),γ′=(1−β)라고 재정의 할 때, 다음과 같은 조건에서 아핀 조합이 만족되어 Plane이 생성된다.
α′+β′+γ′=1\alpha'+\beta'+\gamma'=1α′+β′+γ′=1
T(α′,β′,γ′)=α′P+β′Q+γ′RT(\alpha',\beta',\gamma')= \alpha' P + \beta'Q + \gamma'RT(α′,β′,γ′)=α′P+β′Q+γ′R
참고로 α′,β′,γ′\alpha',\beta',\gamma'α′,β′,γ′를 이용한 점의 표현을 중심좌표(barycentric coordinate) 표현이라고 한다.
Normal Vector
Summary
•
Geometric Primitives
◦
Point, Vector
◦
Affine Combination
•
Others?
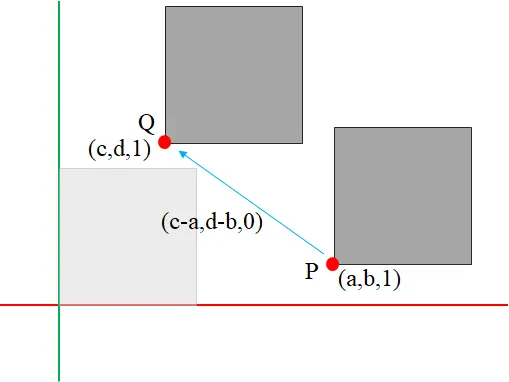
Coordinate Systems for Rendering
월드 좌표 → 스크린 좌표로 변환해줘야 한다.
래스터 디바이스에서는 스캔라인이 있어서 몇번째 스캔라인에 몇번째 점을 업데이트 하는지를 알려줘야한다.
The Problem of Screen Coordinate System
•
움직이는 물체를 어떻게 처리할 것인가?
•
가변 해상도를 어떻게 처리할 것인가?
즉, 좌표를 어떻게 처리해야지 어느 해상도에서라도 동일한 정보를 렌더링할 수 있는가?
⇒ 스크린의 좌표를 표준화하면 되겠구나!
이렇게 표준화된 좌표를 정규화된 좌표(Normalized coordinate)라고 한다.
정규좌표를 이용하면, 스크린 좌표계로 안정적으로쏠 수 있게 될 것이다.
오브젝트 좌표계(벡터 공간?) → 월드좌표계(아핀 공간!) →(차원 변환)→ 정규좌표계 → 스크린 좌표계(픽셀 행)
OpenGL Normalized Coordinate Systems
Rendering Points
Primitives입장에서 점을 보면 다음과 같이 해석될 것이다.
•
2차원의 정규화된 위치 (x,y)
•
컬러
•
절대위치 or 상대위치
Q : 점들로 모든 2D 이미지를 다 나타낼 수 있겠네요?
A : 시간이 너무 오래걸립니다. 저장의 효율성도 높지 않구요.
Remaining Questions
•
점을 픽셀로 바꾸는 과정에서
◦
월드 좌표계에서 정규 좌표계로 어떻게 변환하는가? → 추후 Projection에서 다룸
◦
정규좌표계에서 스크린 좌표계로 어떻게 옮기나?
◦
직선을 어떻게 그릴까?
Rendering Lines
앞서 직선은 두개의 점과 아핀 조합으로 설명이 가능하다.
수학적 좌표계에서는 이걸 그리는게 아주아주 쉽겠지만, 래스터 디바이스에서는 이야기가 조금 달라진다.
두 개의 점을 연결하는 사이의 중간 지점을 어떻게 처리하는가?
Naive Solution
1.
시작점에서 출발한다.
2.
시작점에서 시작점을 제외하고 직선과 거리가 가장 가까운 인접한 픽셀을 고른다.
3.
인접한 픽셀을 기준으로 다시 정한다.
특정 방향으로 가니까 다른 방향의 점은 볼 필요가 없는 것이 특징.
→ 난이도가 낮으나 계산량이 정말 많다.
A bit better algorithm : Line equation
y=mx+by=mx + by=mx+b
p0,p1이 주어진다고 가정했을 때 m, b의 값을 구할 수 있을 것이다.
m = dx/dy = (x2-x1)/(y2-y1)
dx = x2-x1;
dy = y2-y1;

for x from x1 to x2{
		y = y1 + (dy) * (x-x1)/(dx)
		plot(x,y)
}
C++
복사
Naive solution보다는 훨씬 계산량이 줄어들었지만 다음과 같은 문제점이 남아있다.
•
곱셈과 나눗셈이 오버헤드가 크다.
•
계산결과가 소수일 경우 어디를 칠할 지가 헷갈리기 시작해진다.
기본적으로는 Line Equation의 기틀을 유지하면서 계산 오버헤드를 최소화하는 방향으로 알고리즘이 발달해왔다. 아래는 그 예시 중 하나이다.
Digital Differential Analyzer : DDA
dx = x2-x1;
dy = y2-y1;

for x from x1 to x2{
		y = y1 + (dy) * (x-x1)/(dx)
		plot(x,y)
}
C++
복사
기존의 코드를 유심히 보자. x가 1 증가할 때마다, y는 m(=dx/dy)만큼 증가하게 된다.
즉, 코드는 다음과 같이 간략화할 수 있다.
dx = x2-x1;
dy = y2-y1;
m = dx/dy;

for x from x1 to x2{
		y += m;
		plot(x,y)
}
C++
복사
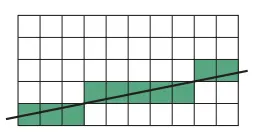
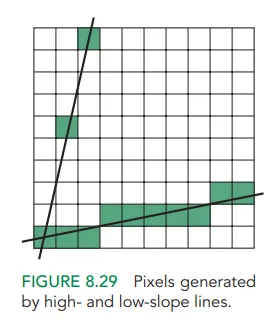
m이 1보다 작은 경우는 y가 몇 픽셀 단위로 1씩 증가하게 된다.
m이 1보다 크게 되면, y값이 위로 크게 튀게 된다. → 선이 뚝뚝 끊겨 보이게되므로 이를 보정해야한다. → y를 for문에 넣어버린다!
dx = x2-x1;
dy = y2-y1;
m = dx/dy;

//m>1
for y from y1 to y2{
		x += 1/m;
		plot(x,y)
}
C++
복사
이 두개를 합친 버젼은 다음과 같다.
lineDDA(Point p0, Point p1){
		d = p0-p1;
		if(d.x > d.y) steps = d.x; else steps = d.y;
		dx = d.x/steps;
		dy = d.y/steps;
		x = p0.x; y = p0.y;
		plot(x,y);
		for(k=0; k<steps; k++){
				x += dx;
				y += dy;
				plot(x,y);
		}
}
C++
복사
만든 사람 천잰데?
m이 1보다 크면 steps는 d.x가 된다. dx=1, dy = m이 되므로 for문 만족.
m이 1보다 작으면 steps는 d.y가 된다. dy=1 dx = 1/m이 되므로 역시 만족.
따라서 모든 경우에 대해서 정상적으로 점이 렌더링되는 것을 확인할 수 있다.
ANOTHER Line Equation
y=ys+m(x−xs)y = y_s + m(x-x_s)y=ys​+m(x−xs​)
m=Δy=(ye−ys)Δx=(xe−xs)m = \cfrac{\Delta y=(y_e-y_s)}{\Delta x=(x_e-x_s)}m=Δx=(xe​−xs​)Δy=(ye​−ys​)​
Δx(y−yi)=Δy(x−xi)\Delta x(y-y_i) = \Delta y(x-x_i)Δx(y−yi​)=Δy(x−xi​)
f(x,y)=Δx(ye−ys)−Δy(xe−xs)=0f(x,y) = \Delta x(y_e-y_s) - \Delta y(x_e-x_s) = 0f(x,y)=Δx(ye​−ys​)−Δy(xe​−xs​)=0
f(x,y)={0when x,y is on the line>0when x,y is above the line<0when x,y is below the linef(x,y) = \begin{cases}0 & \text{when }x,y\text{ is on the line}\\ > 0 & \text{when }x,y\text{ is above the line}\\ < 0 & \text{when }x,y\text{ is below the line}\\ \end{cases}f(x,y)=⎩⎨⎧​0>0<0​when x,y is on the linewhen x,y is above the linewhen x,y is below the line​
Flood Fill : BFS Maze Problem
클리핑으로 해결하나?
Next chapter
3 : OpenGL Primer