🙆‍♀️

Ch.9 B-Spline Curves

course

last review

mastery

intermediate

progress

not started

date

2023/09/26

4 more properties

Previous chapter

Ch.7 Beziers Curves

Today’s MAIN QUEST

Continuity Analysis

C0 Continuity (Positional Continuity)

C1 Continuity (Velocity Continuity)

B-Splines

Knot는 Control Point가 아니다

Bezier Curve VS B-Spline

Reference

Today’s MAIN QUEST

B-Spline에 대해 알아보고, Bezier Curve와의 차이점에 대해 고민해보자.

Continuity Analysis

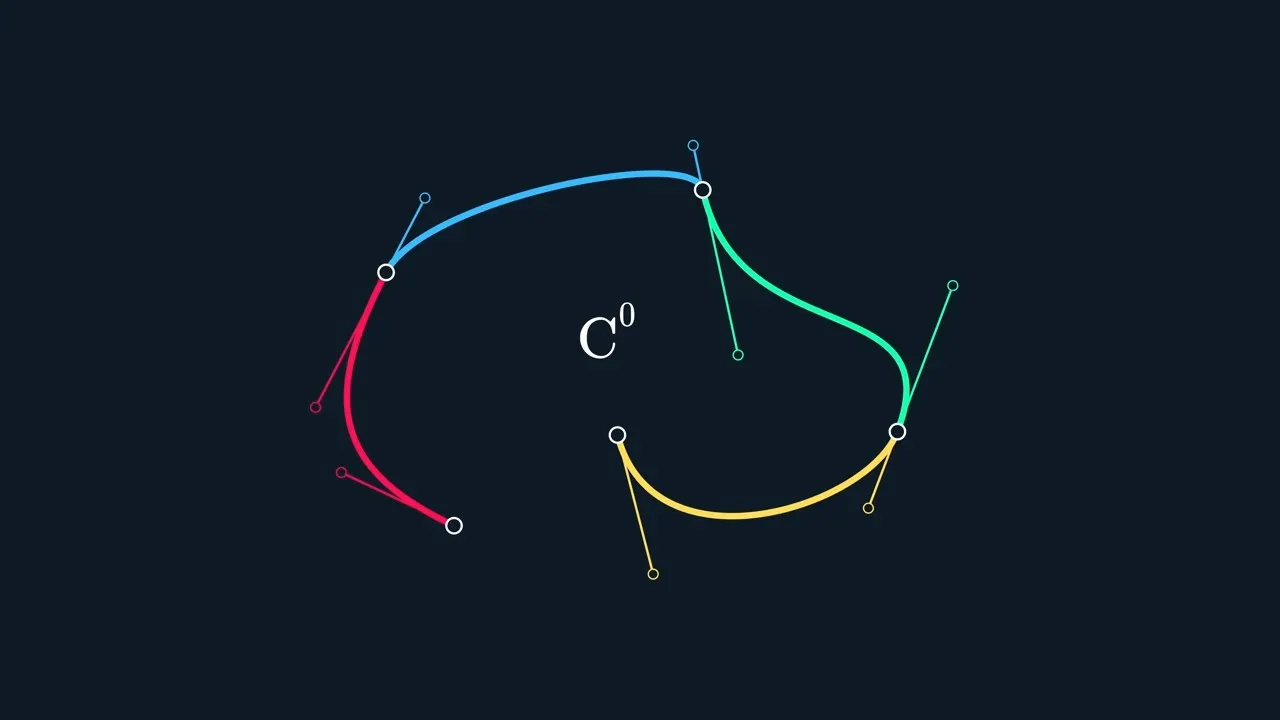
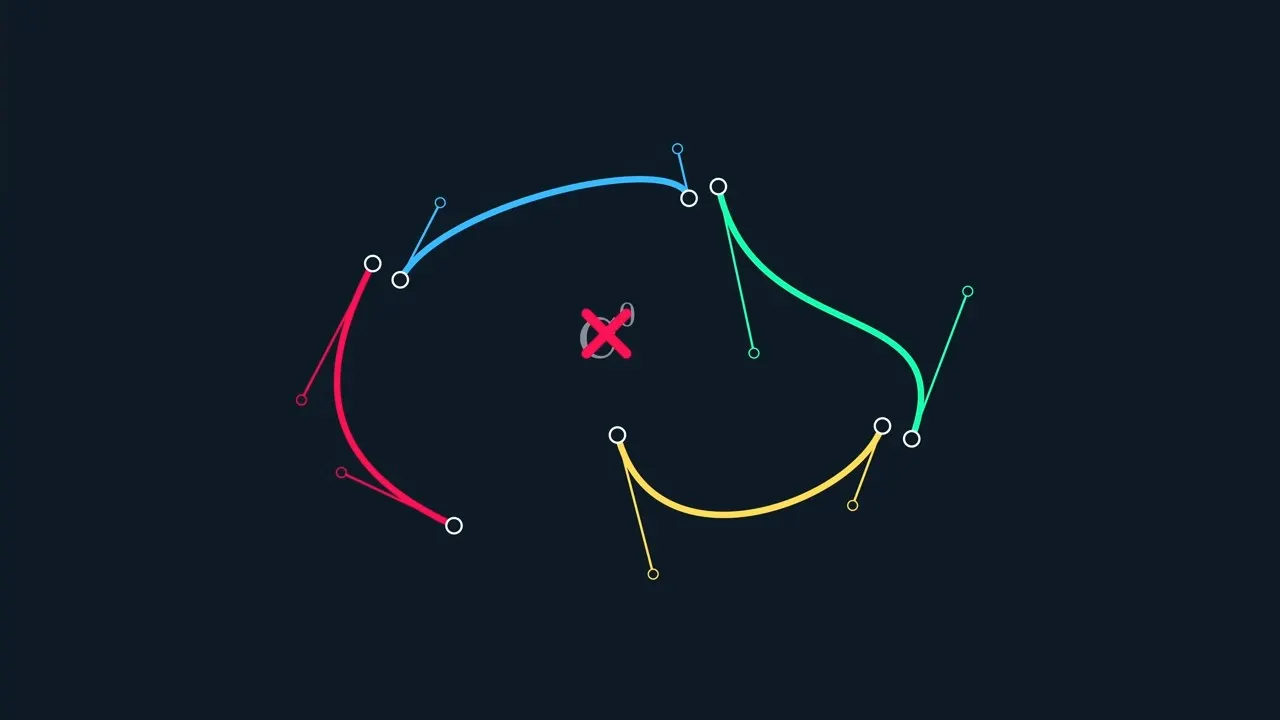
C0 Continuity (Positional Continuity)

C1 Continuity (Velocity Continuity)

B-Splines

n차 Basisfunction을 매개변수 t에 의해 정의된다.

이때 t (0~1)은 m개의 knots로 구성될 수 있다.

B_{i,0}(t)

일때를 살펴보자.

B_{i,0}(t):= \begin{cases}1 & \text{if }t_i\leq t < t_{i+1}, \\ 0 & \text{if }\text{ otherwise} \end{cases}

더 높은 차수에 대해서는 다음과 같이 정의한다.

B_{i,p}(t):= \frac{t-t_i}{t_{i+p}-t_i}B_{i,p-1}(t) + \frac{t_{i+p+1}-t}{t_{i+p+1}-t_{i+1}}B_{i+1,p-1}(t)

이때 각 점화식의 계수가 의미하는 것은 다음과 같다

\frac{t-t_i}{t_{i+p}-t_i}B_{i,p-1}(t)

t-t_i

를

t_{i+p}-t_i

의 길이만큼 나누면

t_i \dots t_{i+p}

까지의 구간 중 현재 t가 해당 구간에 어느 비율의 위치에 있는지를 [0,1]구간으로 나타낸다.

\frac{t_{i+p+1}-t}{t_{i+p+1}-t_{i+1}}B_{i+1,p-1}(t)

마찬가지로

t_{i+p+1}-t

를

t_{i+p+1}-t_{i+1}

의 길이만큼 나누면

t_{i+1} \dots t_{i+p+1}

까지의 구간 중 현재 t가 해당 구간에 어느 비율의 위치에 있는지를 이번에는 [1,0]구간으로 거꾸로 나타낸다.

즉, 해당 Basis Function은 t의 위치에서 각 가중치의 합을 i부터 i+p까지 더하겠다는 의미이다.

그나저나 저 식들 어디서 본 것 같지 않나?

v_M = v_{P_0}\times (1-t) + v_{P_1}\times t

B_{i,p}(t):= \frac{t-t_i}{t_{i+p}-t_i}B_{i,p-1}(t) + \frac{t_{i+p+1}-t}{t_{i+p+1}-t_{i+1}}B_{i+1,p-1}(t)

두 식이 매우 닮은 꼴임을 알 수 있다.

knot 벡터를 정규화한 후, 이전 Basis를 조합한다는 아이디어는 베지어 커브를 일반화한 것과 같은 이야기다!

이런 Basis Function을 각 점에 대해 붙이면 B-Spline 완성이다.

S(t) = \sum^{m-n-2}_{i=0}P_iB_{i,n}(t)

Knot는 Control Point가 아니다

이 Spline을 이해하는데 가장 힘들었던 부분이다. knot는 Control Point가 어디까지 영향을 주는가에 대한 이야기지, Control Point거나, Control Point가 포함된 서브 Control Point가 아니다!!

가령 예를 들어보자.

B_{i,0}(t):= \begin{cases}1 & \text{if }t_i\leq t < t_{i+1}, \\ 0 & \text{if }\text{ otherwise} \end{cases}

이 식을 제대로 이해해보자. 0차일 경우의 Basis Function이다. t가 해당 범위에 있을때, Basis Function은 1이거나 0이다. 이때 knot vector의 개수는 n+1개. 즉 n개의 구간에서 각 i번째 구간일때, T의 위치는 각 컨트롤 포인트로 이산적인 분포를 보인다.

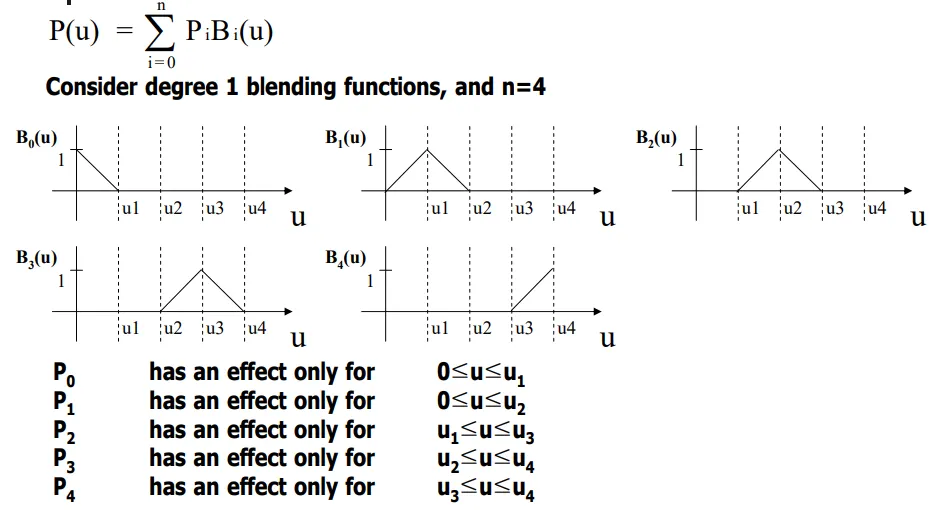
5개의 Control Point가 있는 Linear B-Spline을 살펴본다. 여기서는 Uniform이라 가정한다.

위 슬라이드처럼, Basis Function에 의해 각 컨트롤포인트가 영향을 주는 값은 그래프를, 영향을 주는 범위는 그래프가 양수인 범위만큼이다.

Degree가 1, 컨트롤 포인트가 5개이므로, knot vector의 사이즈는 7이다.

다시 재귀적으로 돌아가보자.

각 컨트롤포인트에 대해서 5개의 Basis Function을 가지기 위해서는, 0차 일 때 6개의 0차 Basis Function을 가져야 한다. 이를 위해서는 7개의 knot Vector가 필요하다.

이때, B0를 무시하고 B1부터 시작한다고 가정하자.(위 그래프는 사실 Non Uniform이다.)

B1이 u1에 도착하기 전까지는 Basis의 총합이 1이 되지 않는다! Affine 좌표계로 확인했을때, 해당 점은 u가 u1에 도착하기까지 z=0축에서 z=1인축으로 서서히 올라오고 있다!!

마찬가지로 B3에서 끝난다고 가정했을때, u3부터 u4까지는 z=1에서 z=0으로 Linear하게 다시 내려가는 모습을 알 수 있다.

이것이 Periodic B-spline이 양 끝점에서부터 그려지지 않는 이유다.

또한, 양 끝점을 연결했을 경우 해당 Basis가 상호보완되어 스플라인이 연결된다는 점이 이 스플라인이 Periodic함을 보이는 또 다른 열쇠임을 보여준다.

Uniform knot vector는 반드시 같은 간격으로 존재한다. Control Point 위에 반드시 존재하지 않으며, knot vector의 개수는 degree + Control Point + 1개로 정해진다.

Bezier Curve VS B-Spline

이렇게 보면 B스플라인은 베지에 커브랑 아무 관련없는 신종 커브인 것처럼 보이지만, 놀랍게도 B-Spline은 일종의 Bezier Curve의 일반화된 버젼이라고 할 수 있다.

곡선의 어느 한 지점 t에서 좌표값을 계산할 때, n개의 Control Point의 가중치의 합으로 계산한다는 점에서 Bezier Curve와 B Spline은 같은 특징을 공유한다.

Reference

[작성중] B-Spline이란?

Spline의 정의와 속성 What is spline? 스플라인(Spline) 이란 원래 "목수들이 부드러운 곡선을 긋기 위해 사용하던 얇은 금속 띠" 라고 한다.[4] 그러나 현대에는 여러 개의 제어점(CP, Control Point)에 영향을 받는 다항식으로 표현된 곡선이라고도 말한다. 대충 상상을 하면 긴 철사를 꺾지 않으면서 중간 중간 원하는 위치에 고정하면 철사의 강성에 따라 다양한 spline 곡선이 나온다. Control Point, Order, Degree and Segment 제어점은 곡선의 모양을 제어하는 특징점이라 할 수 있는데, 점의 추가, 삭제, 변경 등을 통해서 곡선의 형상을 제어한다. 스플라인 함수의 위수(Order) $k$는 다항식 근사를 위해 사용하는 점의 갯수이며 차수(D..

https://stella47.tistory.com/138

Next chapter

Ch.11 Surfaces