Previous chapter
Today’s MAIN QUEST
지금까지 정의한 곡선을 활용하고, 차원을 확장하여 곡면을 정의하자.
Surface
v의 곡선이 만들어내는 점을 Control Point로 하는 새로운 곡선.
Strategy
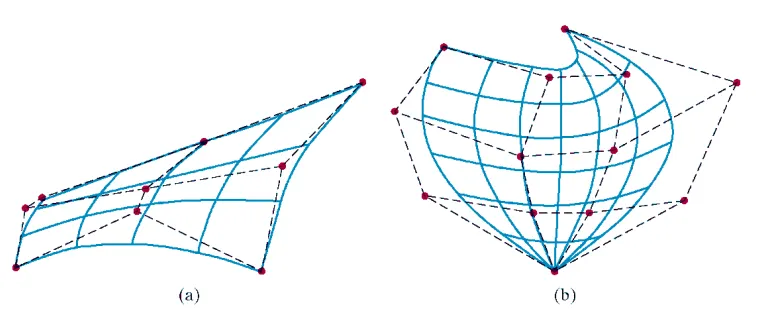
위 곡면이 어떤 곡면인지 맞춰보자.
양 끝 Control Point에 곡선의 끝이 연결되어있기 때문에 Bezier Curve임을 알 수 있다.
혹은 NURB거나.
양 끝 점에 연결되어있지 않다면 Uniform B-Spline일 것이다.
Control Patch
중요한 점은 모든 u와 v값에 대해 어느 한 변수의 값이 정해질 경우, 남은 값에 대해서 Bezier Curve가 성립한다는 점이다.
즉, 모든 Subsection이 베지어 커브다.
Control Point들의 조합으로 표현되는 3차원 좌표 값을 Control Patch라고 한다.
Cubic Bezier Patch
에 대해 4*4개의 Bezier Patch는 컨트롤 포인트를 가진다.
j번째 Control Point 는 다음과 같은 식을 따른다. j가 고정되고, i가 바뀐다.
그럼 다음과 같은 식이 나타난다. j가 고정되었을때, 고정된 j 값에 대한 새로운 컨트롤 포인트 i를 만들어내고, 그 컨트롤 포인트를 활용해 다시 u에 대해 계산한다.
이런 방식을 Bicubic Tensor Product Patch라고 한다.
•
Bezier의 경우에 4개의 코너 컨트롤 포인트를 반드시 지난다.
•
중앙의 4개의 컨트롤 포인트는 중간에 있는 모양만 바꾸지 가장자리의 모양을 바꾸지 않는다. 가장자리는 가장자리의 포인트로 변화시킬 수 있다.
◦
중간포인트로 전반적인 커프의 곡률을 정하고, 가장자리로 곡면의 모양을 정한다.
Continuity
Bezier Patch는 C2 Continuity를 보장하기 매우 어렵다.
Drawing
Basis Function을 사용해서 Bezier Surface Patch를 생성할 수 있다. P가 제어점의 행렬이라고 가정하자.
이제 대응되는 Bezier Surface Patch는 다음과 같다.
Subdivision Surface
Next chapter