Search

Transform

course
last review
mastery
none
progress
not started
date
2023/04/27
4 more properties
Previous chapter

Transform

[x′y′]=[xy]+[ab] \begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} x \\ y \\ \end{bmatrix} + \begin{bmatrix} a \\ b \\ \end{bmatrix}
P′=P+TP' = P + T
현재 좌표 P에 벡터 T를 더해서 새로운 좌표를 만들 수 있다.
움직여야하는 물체가 복잡하다면? 엄청 많은 점의 위치를 일일이 다 바꿔서 다시 바꿔줘야한다.

Rigidbody Transform

물체가 이동할 때 모양이 바뀌지 않는 변환이동을 Rigidbody Transformation이라 한다.

Scaling

x′=xSxy′=ySyx' = xS_{x}\\ y' = yS_{y}
행렬
[x′y′]=[Sx00Sy][xy] \begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} S_{x} & 0 \\ 0 & S_{y} \end{bmatrix} \begin{bmatrix} x \\ y \\ \end{bmatrix}

Rotation

Euler Rotation

회전의 방정식을 써보자.
x′=xcos⁡θ−ysin⁡θy′=xsin⁡θ+ycos⁡θx' = x\cos\theta-y\sin\theta \\ y' = x\sin\theta+y\cos\theta
행렬로 나타내면 다음과 같다.
[x′y′]=[cos⁡θ−sin⁡θsin⁡θcos⁡θ][xy] \begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ \end{bmatrix}
회전 변환은 마찬가지로 강체 변환(Rigidbody Transform)의 성질을 가진다. 즉, 강체의 모습을 그대로 유지하기 위해 3차원 공간의 회전은 세 표준기저벡터가 동일한 크기와 직교성을 유지한 채로 함께 움직여야 한다.
세 표준기저벡터값을 안다면 이를 열벡터로 꽂아넣어 회전 변환행렬 R을 만들 수 있을 것이다.
하지만 위 방법은 매번 3개의 변화하는 표준기저벡터를 계산해야한다. 따라서 이를 해결하기 위해 회전하는 중심축과 각으로 표현된 회전량을 지정하는 오일러 각 방식을 사용한다.
세 표준 기저벡터를 중심으로 회전하는 각을 모으면 다음 3차원 벡터로 표현할 수 있다.
(θx,θy,θz)(\theta_x,\theta_y,\theta_z)
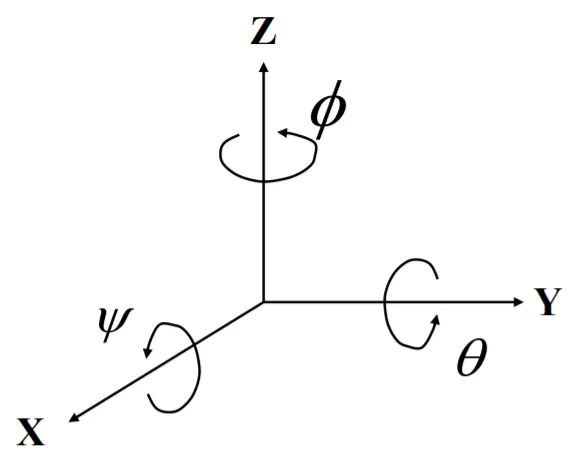
오일러 각은 표준기저벡터를 중심으로 진행되는 세번의 연속적인 회전을 의미한다.
•
X축 회전은 YZ평면의 회전을 의미한다.
◦
x값은 편하지 않고, y와 z의 값만 변한다.
•
Y축 회전은 XZ평면의 회전을 의미한다.
◦
y값은 변하지 않고, x와 z의 값만 변한다.
•
Z축 회전은 XY평면의 회전을 의미한다.
◦
z값은 변하지 않고, x와 y의 값만 변한다.
따라서 각 회전행렬은 다음과 같이 설계가 가능하다.
Rx=[1000cos⁡θ−sin⁡θ0sin⁡θcos⁡θ] R_x =\begin{bmatrix} 1 & 0 & 0 \\ 0&\cos\theta & -\sin\theta \\ 0&\sin\theta & \cos\theta \\ \end{bmatrix}
Ry=[cos⁡θ0sin⁡θ010−sin⁡θ0cos⁡θ] R_y =\begin{bmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \\ \end{bmatrix}
Rz=[cos⁡θ−sin⁡θ0sin⁡θcos⁡θ0001] R_z =\begin{bmatrix} \cos\theta & -\sin\theta&0 \\ \sin\theta & \cos\theta&0 \\ 0&0&1 \end{bmatrix}

Model Matrix

모델의 변환행렬은 다음과 같다.
S=[sx0000xy0000sz00001]S = \begin{bmatrix} s_x&0&0&0 \\ 0&x_y&0&0 \\ 0&0&s_z&0 \\ 0&0&0&1 \end{bmatrix}
R=[xxyxzx0xyyyzy0xzyzzz00001]R = \begin{bmatrix} x_x&y_x&z_x&0 \\ x_y&y_y&z_y&0 \\ x_z&y_z&z_z&0 \\ 0&0&0&1 \end{bmatrix}
T=[100tx010ty001tz0001]T = \begin{bmatrix} 1&0&0&t_x \\ 0&1&0&t_y \\ 0&0&1&t_z \\ 0&0&0&1 \end{bmatrix}
이 세 행렬을 TRS 연산 순서에 따라 곱해 만든 모델링 행렬 M은 다음과 같이 계산된다.
M=T⋅R⋅S=[xxsxyxsyzxsztxxysxyysyzysztyxzsxyzsyzzsztz0001]M = T \sdot R \sdot S = \begin{bmatrix} x_xs_x&y_xs_y&z_xs_z&t_x \\ x_ys_x&y_ys_y&z_ys_z&t_y \\ x_zs_x&y_zs_y&z_zs_z&t_z \\ 0&0&0&1 \end{bmatrix}

Cross Product

벡터의 외적이란 참 신기한 친구다. 내적이 모든 차원에 적용가능한 것과는 달리, 외적은 반드시 3차원 공간에서만 사용가능하기 때문이다.

Basics

u⃗=(ux,uy,uz),v⃗=(vx,vy,vz)u⃗×v⃗=(uyvz−vyuz,uzvx−vzux,uxvy−vxuy)\vec u = (u_x,u_y,u_z), \vec v = (v_x, v_y, v_z)\\ \vec u \times \vec v = (u_yv_z-v_yu_z, u_zv_x-v_zu_x, u_xv_y-v_xu_y)
외적은 회전의 순환순서 x→y→z→x→yx \rightarrow y \rightarrow z \rightarrow x \rightarrow y에 맞춰 벡터를 순서대로 나열하는 형태이다.
또한 외적의 결과는 언제나 3차원 벡터가 된다. 내적이 항상 스칼라로 나오는 것과 대비된다.
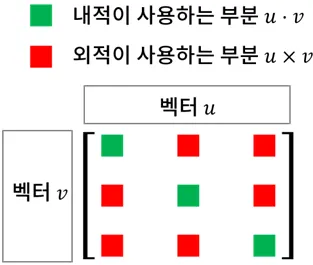
외적 계산식의 패턴은 특정 성분의 결과를 만들기 위해 그 성분과 하등 관련없는 나머지 두 성분을 결합한다는 점이 특징이다.
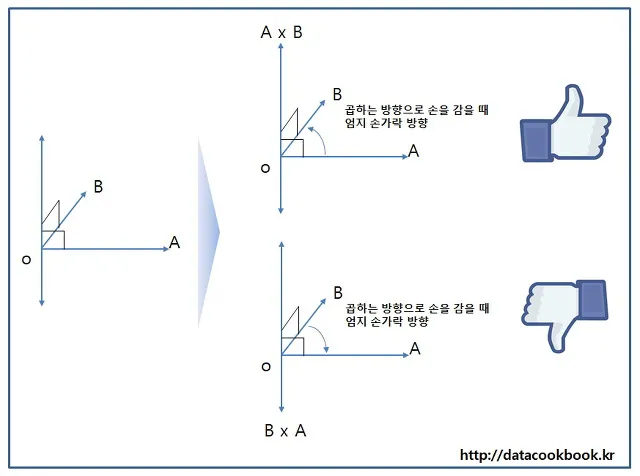
외적은 교환법칙이 성립되지 않는다. 전개식에 뺄셈이 있기 때문이다. 뺄셈도 순서를 바꾸면 반대수가 나오는 것 처럼 외적도 순서를 바꾼다면 방향이 반대로 나오게 된다.
u⃗×v⃗=−v⃗×u⃗\vec u \times \vec v = -\vec v \times \vec u
또한 외적은 결합법칙이 성립하지 않는다. 다만 덧셈의 분배법칙만 성립한다.
내적
외적
계산결과
스칼라
벡터
교환법칙
성립함
성립하지 않음
결합법칙
성립하지 않음
성립하지 않음
분배법칙
성립함
성립함
연산 방법
같은 위치의 요소만 사용
다른 위치의 요소만 사용

평행성 판별

동일한 벡터끼리 내적을 진행하면 벡터 크기를 제곱한 값이 나온다. 그럼 외적은?
임의의 벡터 u⃗\vec u값을 (ux,uy,uz)(u_x,u_y,u_z)라고 정의하고 같은 벡터를 외적하면 그 결과는 항상 영벡터가 나온다.
u⃗×u⃗=(uyuz−uyuz,uzux−uzux,uxuy−uxuy)=(0,0,0) \vec u \times \vec u = (u_yu_z-u_yu_z, u_zu_x-u_zu_x, u_xu_y-u_xu_y) = (0,0,0)
반대방향의 벡터를 외적하더라도 같다.
u⃗×−u⃗=(−uyuz+uyuz,−uzux+uzux,−uxuy+uxuy)=(0,0,0) \vec u \times -\vec u = (-u_yu_z+u_yu_z, -u_zu_x+u_zu_x, -u_xu_y+u_xu_y) = (0,0,0)
그럼 평행하지만 크기가 다른 벡터는 어떨까?
u⃗=(ux,uy,uz),v⃗=ku⃗=(kux,kuy,kuz)u⃗×v⃗=(kuyuz−kuyuz,kuzux−kuzux,kuxuy−kuxuy)\vec u = (u_x,u_y,u_z), \vec v=k\vec u = (ku_x, ku_y, ku_z)\\ \vec u \times \vec v = (ku_yu_z-ku_yu_z, ku_zu_x-ku_zu_x, ku_xu_y-ku_xu_y)
평행한 두 벡터를 외적하면 항상 영벡터가 됨을 알 수 있다.
u⃗\vec u벡터를 v⃗\vec v에 수평인 벡터와 수직인 벡터 u∥⃗,u⊥⃗\vec {u_\parallel},\vec {u_\bot}으로 분해해보자.
u⃗=u∥⃗+u⊥⃗\vec u = \vec {u_\parallel}+\vec {u_\bot}
수평성분과 수직 성분의 덧셈으로 분리 가능하다.
외적은 덧셈의 분배법칙이 성립하므로 다음과 같이 나타낼 수 있다.
v⃗×u⃗=v⃗×(u∥⃗+u⊥⃗)=v⃗×u∥⃗+v⃗×u⊥⃗\vec v \times \vec u = \vec v \times(\vec {u_\parallel}+\vec {u_\bot}) =\vec v \times \vec {u_\parallel}+ \vec v \times \vec {u_\bot}
u∥⃗\vec {u_\parallel}는 v⃗\vec v에 평행하므로 0이 된다. 따라서 위 식은 다음과 같이 축소 가능하다.
v⃗×u⃗=v⃗×u⊥⃗\vec v \times \vec u = \vec v \times \vec {u_\bot}
외적은 상대방에 직교하는 벡터 성분만 사용하는 성질이 있음을 알 수 있다. 즉, 외적의 크기는 sin함수에 비례함을 알 수 있다.
∣u⃗×v⃗∣2=(u⃗×v⃗)⋅(u⃗×v⃗)=(uyvz−uzvy)2+(uzvx−uzvx)2+(uxvy−uxvy)2=uy2vz2−2uyuzvyvz+uz2vy2+uz2vx2−2uzuxvzvx+ux2vz2ux2vy2−2uxuyvxvy+uy2vx2\begin{align*} |\vec u \times \vec v|^2 &= (\vec u \times \vec v)\sdot (\vec u \times \vec v)\\ &=(u_yv_z-u_zv_y)^2+(u_zv_x-u_zv_x)^2+(u_xv_y-u_xv_y)^2\\ &=u_y^2v_z^2-2u_yu_zv_yv_z+ u_z^2v_y^2+ u_z^2v_x^2-2u_zu_xv_zv_x+u_x^2v_z^2 u_x^2v_y^2- 2u_xu_yv_xv_y+u_y^2v_x^2 \end{align*}
(∣u⃗∣∣v⃗∣)2=(ux2+uy2+uz2vx2+vy2+vz2)2=(ux2+uy2+uz2)(vx2+vy2+vz2)=ux2vx2+ux2vy2+ux2vz2+uy2vx2+uy2vy2+uy2vz2+uz2vx2+uz2vy2+uz2vz2\begin{align*} (|\vec u||\vec v|)^2 &=\left(\sqrt{u_x^2+u_y^2+u_z^2}\sqrt{v_x^2+v_y^2+v_z^2}\right)^2\\ &=(u_x^2+u_y^2+u_z^2)(v_x^2+v_y^2+v_z^2)\\ &=u_x^2v_x^2+u_x^2v_y^2+u_x^2v_z^2+u_y^2v_x^2+u_y^2v_y^2+u_y^2v_z^2+u_z^2v_x^2+u_z^2v_y^2+u_z^2v_z^2 \end{align*}
(u⃗⋅v⃗)=(uxvx+uyvy+uzvz)2=ux2vx2+uy2vy2+uz2vz2+2uxuyvxvy+2uyuzvyvz+2uxuzvxvz\begin{align*} (\vec u \sdot \vec v) &=(u_xv_x+u_yv_y+u_zv_z)^2 \\ &= u_x^2v_x^2+u_y^2v_y^2+u_z^2v_z^2+2u_xu_yv_xv_y+2u_yu_zv_yv_z+2u_xu_zv_xv_z \end{align*}
세 식을 조합하면 다음 관계가 성립한다.
∣u⃗×v⃗∣2=(∣u⃗∣∣v⃗∣)2−(u⃗⋅v⃗)2=(∣u⃗∣∣v⃗∣)2−(u⃗v⃗cos⁡θ)2=(∣u⃗∣∣v⃗∣)2(1−cos⁡2θ)=(∣u⃗∣∣v⃗∣)2(sin⁡2θ)\begin{align*} |\vec u \times \vec v|^2 &=(|\vec u||\vec v|)^2 - (\vec u \sdot \vec v)^2 \\ &= (|\vec u||\vec v|)^2 - (\vec u \vec v\cos\theta)^2\\ &= (|\vec u||\vec v|)^2(1-\cos^2\theta)\\ &= (|\vec u||\vec v|)^2(\sin^2\theta)\\ \end{align*}
내적
외적
판별성
직교성
평행성
삼각함수
코사인
사인

Normal Vector

벡터 외적이 가지는 중요한 성질은 두 벡터에 직교하는 벡터를 생성한다는 것이다.
그런데 외적은 교환법칙이 성립하지 않기 때문에 연산의 순서를 바꾼다면 반대 방향으로 향하는 법선 벡터가 생성된다. 따라서 법선 벡터를 생성할 때는 외적의 연산 순서에 신경을 써야한다.
3차원 공간에서 평면은 앞면과 뒷면으로 구성되어 있기 때문이다. 오른손 좌표계를 사용한다면 오른손 법칙을 통해서 방향을 확인할 수 있다. 오른손 좌표계는 CCW가 위쪽방향, CW가 아래쪽 방향이다.
OpenGL은 오른손 좌표계이므로, CCW로 위를 판별하자.

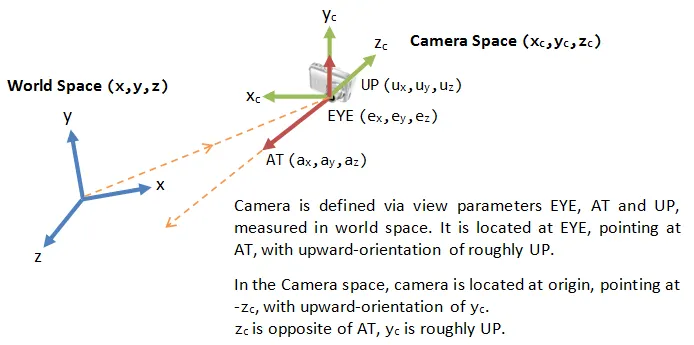
View Matrix

외적을 사용해 카메라의 시선 벡터 정보로부터 카메라의 세가지 로컬 축을 구하고 이로부터 회전행렬까지 얻어낼 수 있다.

Local Z

물체의 위치에서 카메라 위치를 뺀 후 크기를 1로 정규화시킨 벡터를 생성한다.
이 벡터는 카메라 트랜스폼의 로컬 z축이 된다.

Local X

로컬Z축과 월드Y축을 외적하면, 로컬X축을 얻는다.
간단하지만 좋은 묘책이다.

Local Y

로컬Z축과 로컬X축을 외적하면 로컬Y축을 얻는다.
x⃗=u⃗×z⃗∣u⃗×z⃗∣y⃗=z⃗×x⃗z⃗=v⃗∣v⃗∣\begin{align*} \vec x &= \cfrac{\vec u \times \vec z}{|\vec u \times \vec z|}\\ \vec y &= \vec z \times \vec x\\ \vec z &= \cfrac{\vec v}{|\vec v|} \end{align*}
그렇다면 카메라 트랜스폼의 회전행렬 R은 로컬벡터를 열벡터로 지정해 다음과 같이 생성할 수 있다.
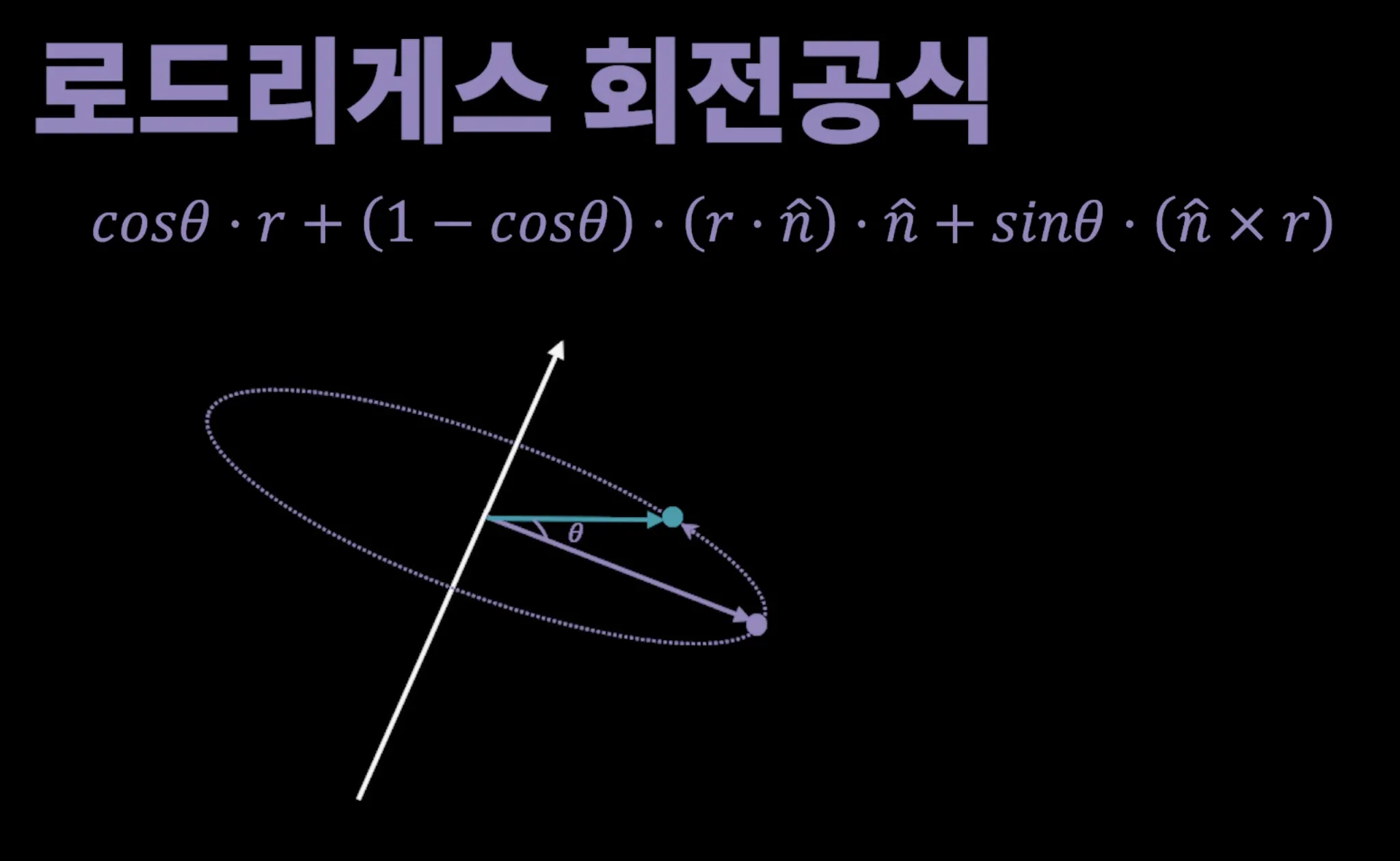
R=[xxyxzx0xyyyzy0xzyzzz00001]R = \begin{bmatrix} x_x&y_x&z_x&0 \\ x_y&y_y&z_y&0 \\ x_z&y_z&z_z&0 \\ 0&0&0&1 \end{bmatrix}

Rodrigues Rotation Formula

오일러 각은 짐벌락 현상이 발생하고 회전 보간이 어렵다는 문제가 있다. 이를 해결하기 위해 임의의 축에 대한 평면의 회전 방식을 사용하면 해결이 가능하다. 이를 Axis-Angle Rotation이라고 부른다.
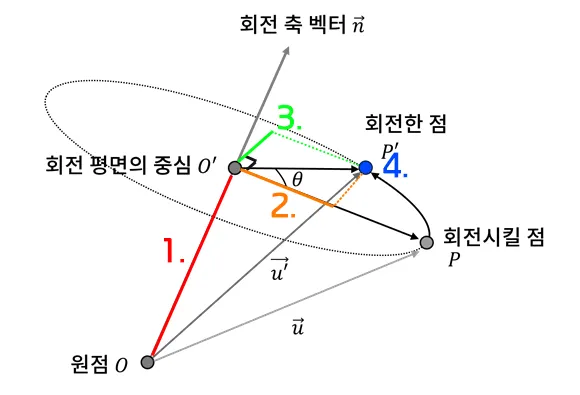
윗 그림과 같이 점과 벡터에 기호를 붙였다. 회전이 발생하는 평면에 직교하는 법선 벡터를 회전축이라고 부르자. 그 회전 축에 의해 회전될 점을 P, 이동한 점은 P’, 월드공간의 원점을 O로, 회전평면의 중심을 O’라고 하자. 점 P의 좌표를 다음과 같이 설정하자.
P=(x,y,z,1)P=(x,y,z,1)
그러고 나서 원점 O에서부터 P까지의 벡터를 u⃗\vec u라고 하자.
u⃗=P−O=(x,y,z,0)\vec u = P-O = (x,y,z,0)
원점O로부터 회전평면중심 O’까지의 벡터를 v⃗\vec v라고 하자. v⃗\vec v는 다음과 같이 계산된다.
OO′→=v⃗=(u⃗⋅n^)⋅n^\overrightarrow{OO'}=\vec v = (\vec u \sdot \hat n) \sdot \hat n
v′⃗=∣v′⃗∣⋅v^=∣v′⃗∣⋅v⃗∣v⃗∣=∣u⃗∣⋅cos⁡θ⋅v⃗∣v⃗∣=∣u⃗∣⋅u⃗⋅v⃗∣u⃗∣∣v⃗∣⋅v⃗∣v⃗∣=(u⃗⋅v⃗)∣v⃗∣2⋅v⃗=(u⃗⋅v⃗)(v⃗⋅v⃗=1)⋅v⃗=(u⃗⋅v^)⋅v^(∵∣v⃗∣=1)\begin{align*} \vec {v'} &= |\vec {v'}|\sdot \hat v\\ &= |\vec {v'}|\sdot \cfrac{\vec v}{|\vec v|}\\ &= |\vec {u}|\sdot \cos\theta \sdot\cfrac{\vec v}{|\vec v|}\\ &= |\vec {u}|\sdot \cfrac{\vec u \sdot \vec v}{|\vec u||\vec v|} \sdot\cfrac{\vec v}{|\vec v|}\\ &=\cfrac{(\vec u \sdot \vec v)}{|\vec v|^2} \sdot\vec v\\ &=\cfrac{(\vec u \sdot \vec v)}{(\vec v \sdot \vec v = 1)} \sdot\vec v\\ &=(\vec u \sdot \hat v) \sdot\hat v (\because |\vec v| = 1) \end{align*}
그럼 회전평면의 중앙으로부터 점 P까지의 거리는 다음과 같다.
O′P→=u⃗−v⃗\overrightarrow{O'P} = \vec u - \vec v
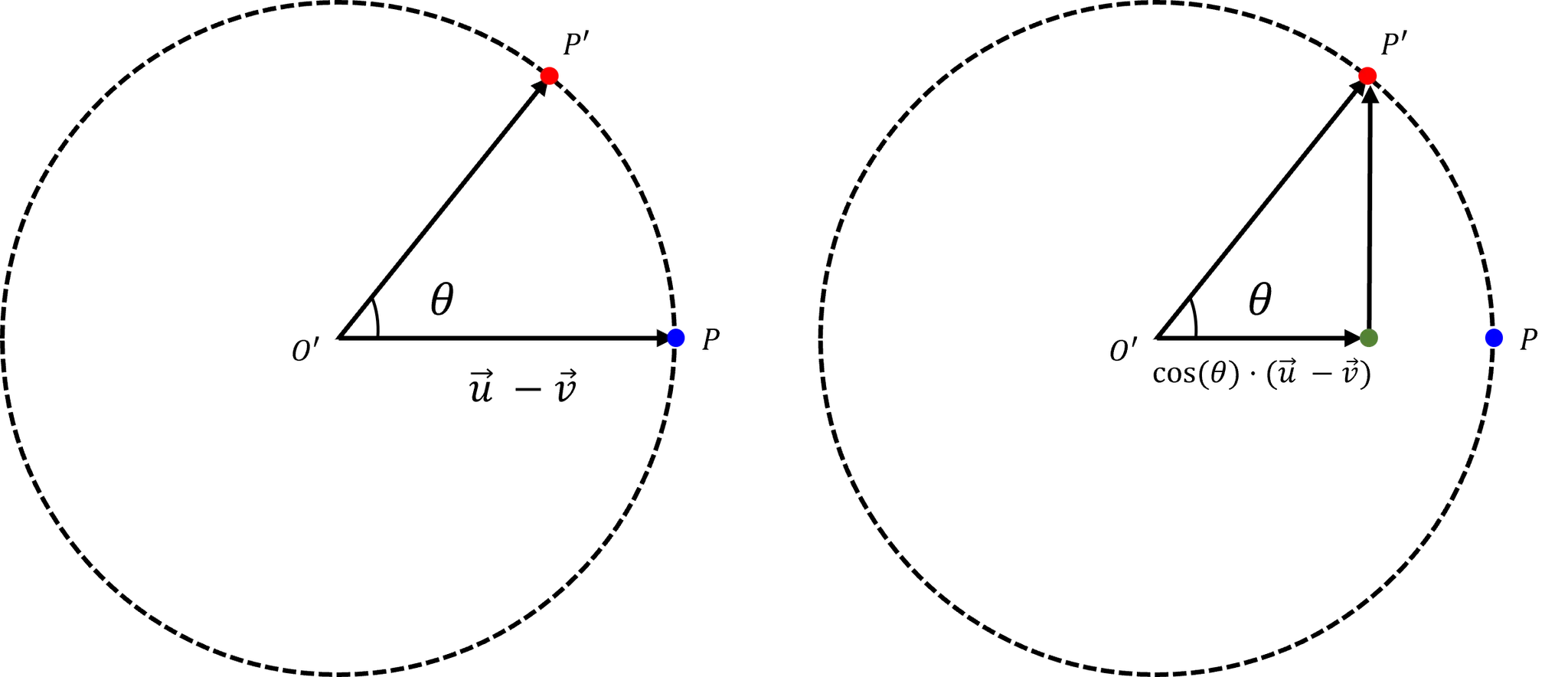
회전평면의 관점에서 보면 다음과 같이 표시된다.
우리가 지금 궁금한 건 O′P′→\overrightarrow{O'P'}이므로, θ\theta값을 이용해서 O′P′→\overrightarrow{O'P'}를 구한다.
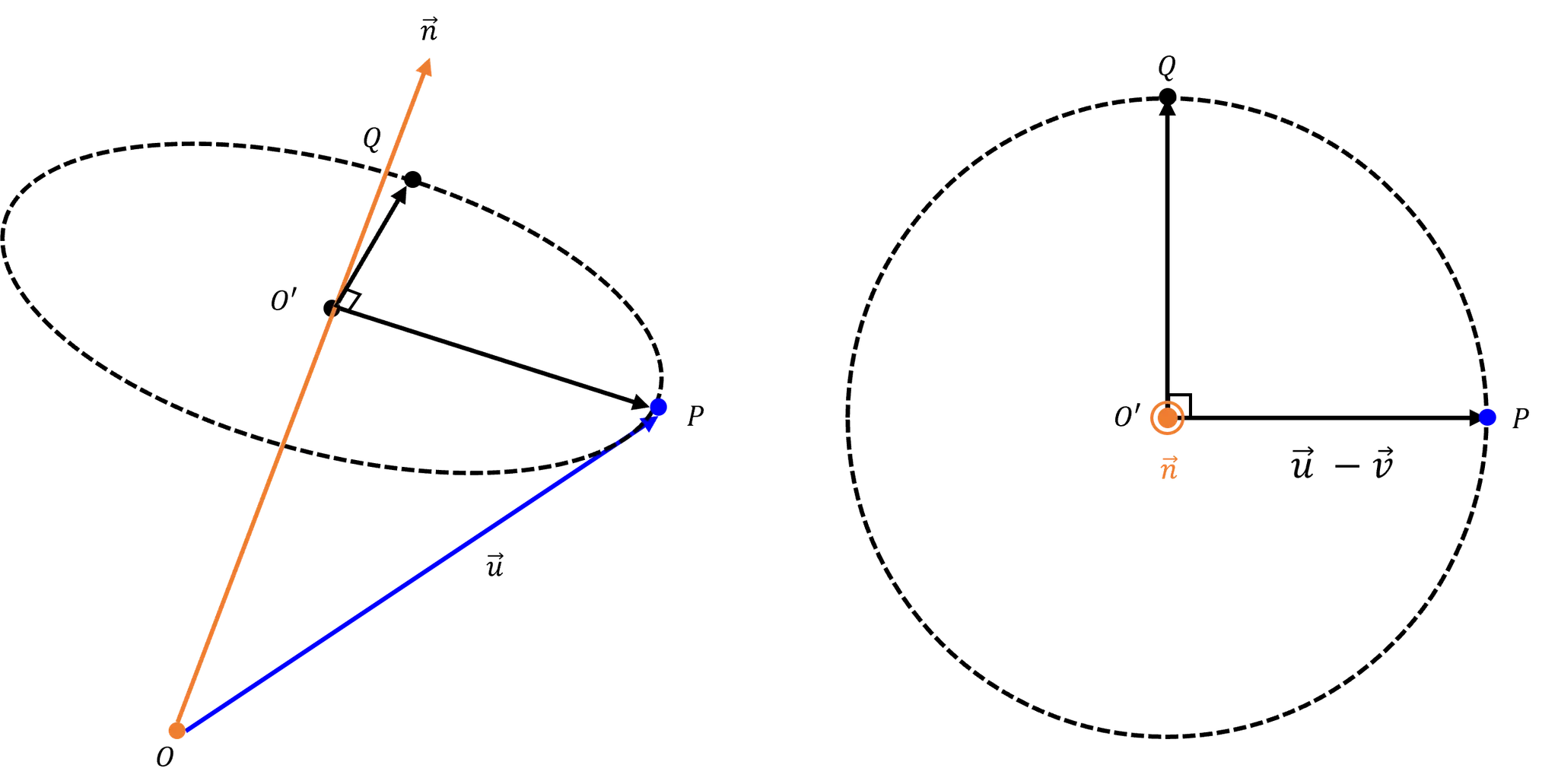
O′P′→\overrightarrow{O'P'}를 가로 성분과 세로성분으로 분리하면, 가로 성분에 해당하는 벡터는 위 그림과 같이 얻을 수 있다.
그리고 O′P→\overrightarrow{O'P}와 OO′→\overrightarrow{OO'}에 수직이면서 회전평면에 소속된 O′Q→\overrightarrow{O'Q}를 구해 세로성분을 구한다.
O′Q→\overrightarrow{O'Q}는 O′P→\overrightarrow{O'P}와 OO′→\overrightarrow{OO'}를 외적하여 구할 수 있다.
O′Q→=n^×(u⃗−v⃗)\overrightarrow{O'Q} = \hat n\times (\vec u - \vec v)
이제 세로 성분을 구하면 된다.
O′P′→=cos⁡θ⋅O′P→+sin⁡θ⋅O′Q→\overrightarrow{O'P'} = \cos\theta\sdot\overrightarrow{O'P} +\sin\theta\sdot\overrightarrow{O'Q}
O′P′→=cos⁡θ⋅(u⃗−v⃗)+sin⁡θ⋅(n^×(u⃗−v⃗))\overrightarrow{O'P'} = \cos\theta\sdot(\vec u - \vec v) +\sin\theta\sdot(\hat n\times (\vec u - \vec v))
n과 v의 외적값은 수직이므로 0이다.
O′P′→=cos⁡θ⋅(u⃗−v⃗)+sin⁡θ⋅(n^×u⃗)\overrightarrow{O'P'} = \cos\theta\sdot(\vec u - \vec v) +\sin\theta\sdot(\hat n\times \vec u)
이제 최종벡터 OP′→\overrightarrow{OP'}는 O′P′→\overrightarrow{O'P'}에 v⃗\vec v를 더한 값이 된다.
OP′→=v⃗+cos⁡θ⋅(u⃗−v⃗)+sin⁡θ⋅(n^×u⃗)\overrightarrow{OP'} = \vec v +\cos\theta\sdot(\vec u - \vec v) +\sin\theta\sdot(\hat n\times \vec u)
벡터 v⃗\vec v를 (u⃗⋅n^)⋅n^(\vec u \sdot \hat n) \sdot \hat n으로 치환하면 최종 식이 완성된다.
OP′→=cos⁡θ⋅u⃗+(1−cos⁡θ)(u⃗⋅n^)⋅n^+sin⁡θ⋅(n^×u⃗)\overrightarrow{OP'} = \cos\theta\sdot\vec u +(1 - \cos\theta)(\vec u \sdot \hat n)\sdot \hat n +\sin\theta\sdot(\hat n\times \vec u)
Next chapter