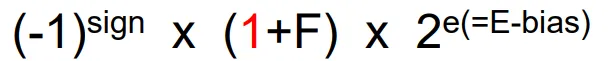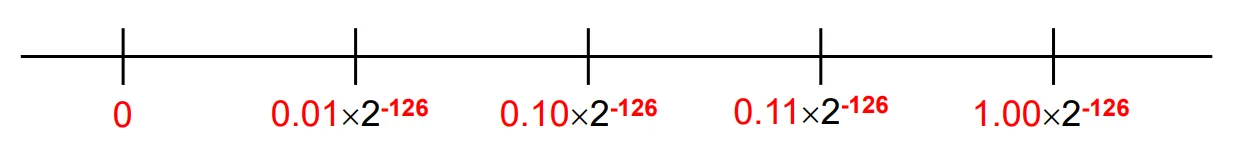Previous chapter
Representing Big & Small Numbers
엄청 큰 수나 엄청 작은 수를 표현하려면 32-bit 정수 표현으로 인코딩하기에는 어림도 없다. 그러면 어떻게 표현해야 할까? 그래서 이때 Floating Number를 사용하여 표현할 것이다.
Floating Point Representation
Floating Point
비 정수를 위한 넘버
•
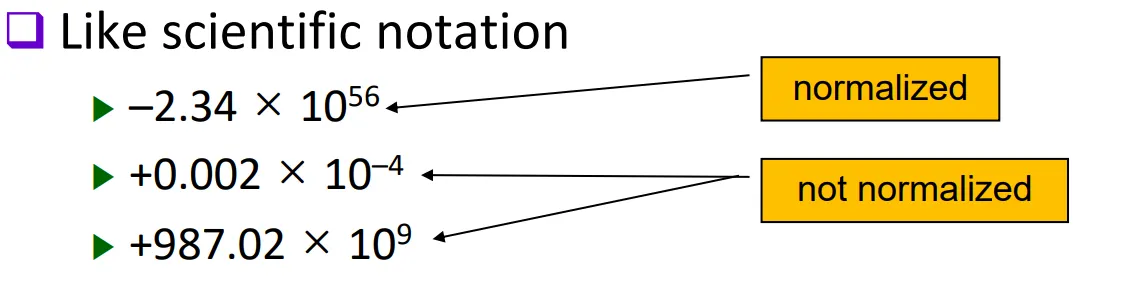
정규화된 표현(normalized)이란 정수의 자릿수가 1자리뿐인 수를 뜻한다.
•
비정규화된 표현(not normalized)이란 정수의 자릿수가 1이 아닌 표현법을 뜻한다.
컴퓨터공학이므로, 이진수 표현으로 나타내면 다음과 같다.
x에 해당하는 수를 fraction number, y를 지수(exponent number)라고 한다.
Representing
32비트 안에 해당 표현을 모두 다해야 한다.
베이스 넘버는 당연하게도 2(10이 아니다!) FPALU?의 디자인에 의해 고정되어있다.
•
E의 범위가 넓어지면 넓은 범위의 수를 표현할 수 있따.
•
F의 범위가 넓어지면 수의 정밀도가 증가한다.
E와 F의 범위가 사람마다 제멋대로면 호환성에 문제가 생긴다!
이를 해결하기 위해 IEEE-754라는 표준이 도입되었다.
IEEE-754
•
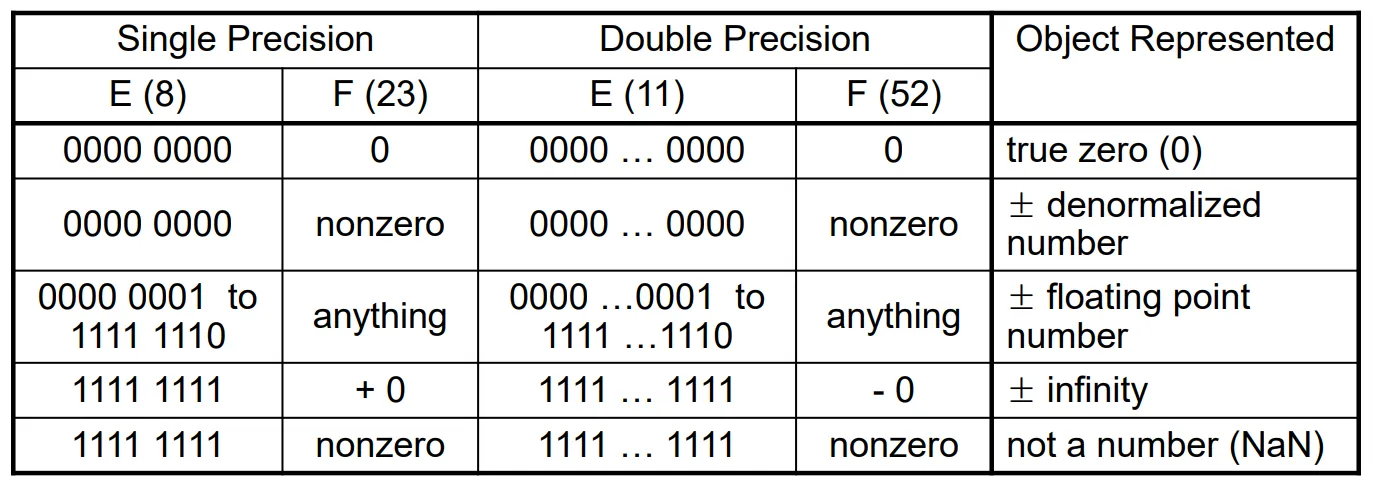
Single Precision : 32-bit : (1,8,23)
•
Double Precision : 64-bit : (1,11,52)
•
빨간색 1은 magnitude Number(1의 자리의 수가 항상 1이 되므로 이를 생략하여 fraction의 정밀도를 더 올리는게 합리적이다!)
•
e는 E-bias ⇒ E를 표현하기 위해서는 e+bias로 계산하자.
•
bias Number는 각각 2^exp-1다.
◦
single : 2^7 = 128
◦
doubl : 2^10 = 1024
Example
-0.75
sign bit = 1
Floating point에서는 sll srl가 적용되지 않는다!
IEEE-754 Normalized form
E : 0000 0001 ~ 1111 1110까지만 Normalized form이다.
F : Any
Example
Smallest+ : 0 00000001 1.00000000000000000000000 = 1 * 2^{1-127}
Largest+ : 0 11111110 1.11111111111111111111111 =
1.0_2 * 2^-1 : 0 01111110 1.00000000000000000000000
0.75_10 * 2^4 = 1.1_2 * 2^3 : 0 10000010 1.10000000000000000000000
Normalized Form에는 Hidden Number 1. 이 숨어있다. 따라서 Normalized Form에는 0을 표현할 수 없다.
그렇다면 0을 어떻게 표현할까?
IEEE-754 Statndard Encoding
Denormal Numbers
•
Exponent = 000…0 일경우 Hidden bit이 0이 된다.
Denormalized Nuber의 영역 [0, 1.00*2^-126)은 fraction에 의해 모든 수가 결정되며, 간격은 일정하다.
•
Exponent = 111…1일 경우 다음과 같은 경우가 생길 것이다.
◦
Fraction = 000…0일 경우
▪
Infinity
•
Fraction ≠ 000…0일 경우
◦
NaN(Not-a-Number)
◦
Exception Events in Floating Point
•
Overflow : Floating point로 표현할 수 없는 (절대값이)큰
•
Underflow : Floating point로 표현할 수 없는 너무 작은 수 (0은 아니나 표현할 수 없음!)
Support for Accurate Arithmetic
•
무조건 Round Up
•
무조건 Round Down
•
Truncate
•
Round to Nearest Even
◦
이진 계산일 경우 중간값인 100…을 기준으로 판단할 것!
Next chapter