Previous chapter
Data Transmission
What we've got here is failure to communicate.
성공적인 데이터 전송은 두 요소에 의해 결정된다.
1.
고품질의 시그널이 전송된다.
2.
전송 매체의 특성
Terminology
데이터는 Transmitter와 Receiver 사이에서 전송매체(Transmission medium)를 통해 이루어진다.
Transmission Medium || 전송 매개체
•
Guided Media는 유선 미디어를 뜻한다. 물리적 통로를 따라 유도되는 전송 매개체
◦
Twisted pair, 동축케이블, 광섬유 등..
•
Unguided media는 무선 미디어를 뜻한다. 전자파를 송신하는 방법을 사용한다.
◦
공기, 진공, 해수 등을 통해 전파된다.
이렇게 전송매개체를 통해 Transmitter → Receiver로 데이터가 전송되는데, 중간에 신호를 증폭하는 증폭기나 리피터 외의 다른 중간 디바이스 없이 송신측에서 수신측으로 직접 데이터가 전송되는 경로를 직접 링크(Direct Link)라고 한다.
•
Guided Media가 Direct Link를 제공해주며, 오로지 두 디바이스만이 링크를 공유하는 경우를 Point to Point이라고 한다.
•
반대로 Multi Point는 Guided Media가 Direct Link를 제공해주지만, 세 디바이스 이상이 링크를 공유하는 경우를 말한다.
통신은 세 방식 중 하나를 채택한다.
•
Simplex || 단방향 통신
◦
오직 한 방향으로만 전송이 가능하며, 하나는 송신기, 하나는 수신기가 된다.
•
Half Duplex || 반이중 통신
◦
양쪽으로 모두 송수신이 가능하나, 동시에 서로 신호교환이 되지 않는다.
•
Full Duplex || 전이중 통신
◦
양쪽으로 모둗 송수신이 가능하며, 동시에 서로 신호를 쏠 수 있다.
강슬설1
강슬설2
Frequency Spectrum and Bandwidth
신호는 시간의 함수이지만, 주파수의 함수로도 표현될 수 있다.
즉, 신호는 여러개의 서로 다른 주파수의 조합으로 구성된다고 볼 수 있다.
데이터 통신에서는 주파수의 관점으로 보는 것이 시간 관점으로 보는 것 보다 훨씬 중요하다.
Time Domain Concepts || 시간영역의 관점
•
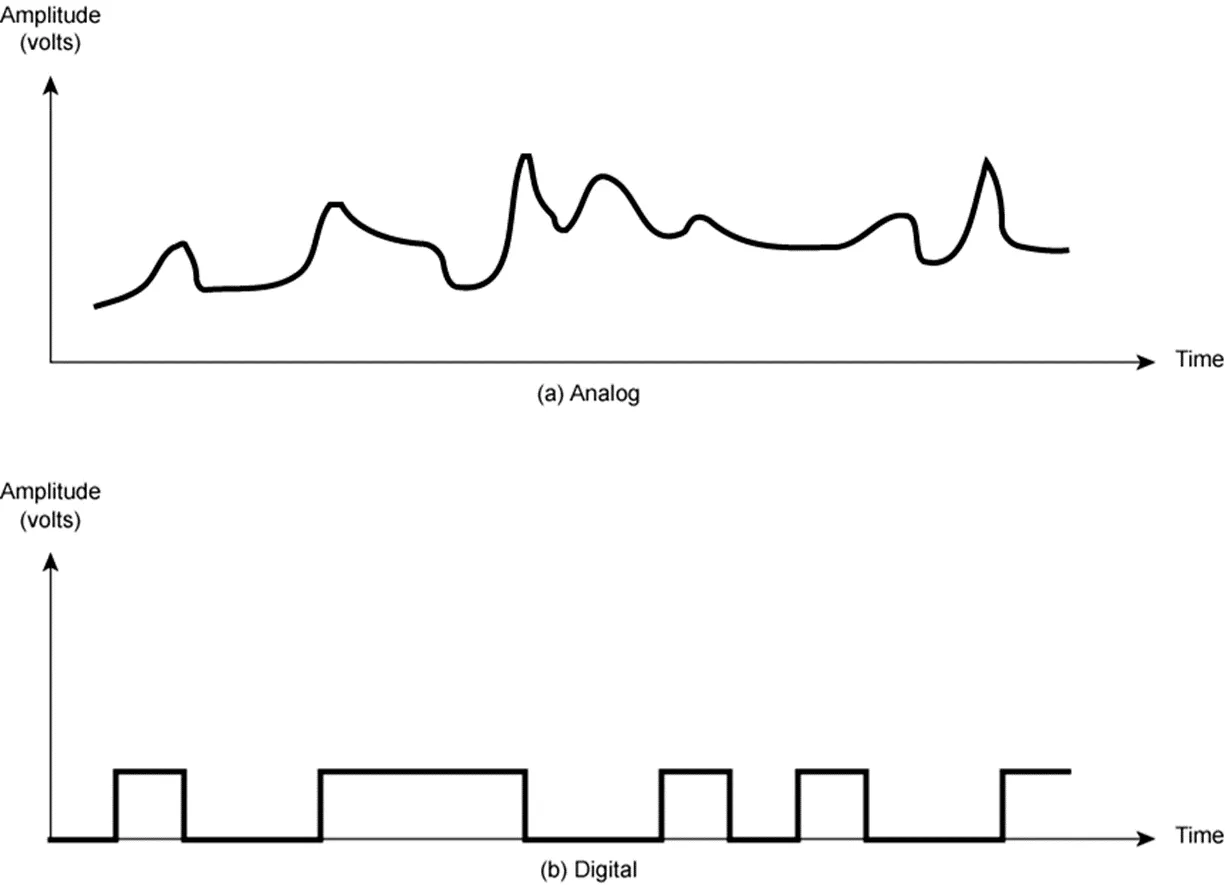
Analog Signal || 아날로그 신호
◦
아날로그 신호는 신호의 세기가 시간에 따라 서서히 지나는 모든 구간이 연속적인 신호다.
•
Digital Signal : 디지털 신호
◦
디지털 신호는 신호의 세기가 일정 기간 동안 일정하다가 갑자기 다른 값으로 변한다.
•
Periodic Signal || 주기신호
◦
동일한 신호 모양이 일정 시간 계속 반복되는 신호를 주기신호라고 한다.
•
Aperiodic Signal || 비주기(?) 신호
◦
신호가 반복되지 않는 경우
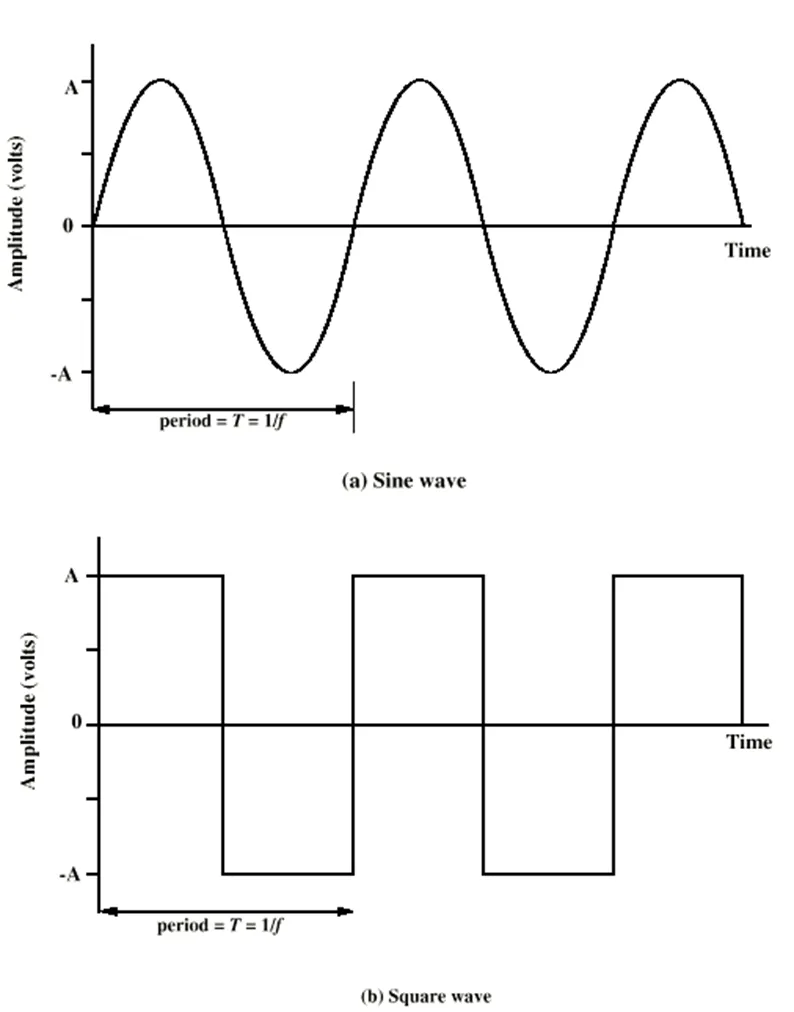
SINE WAVE
•
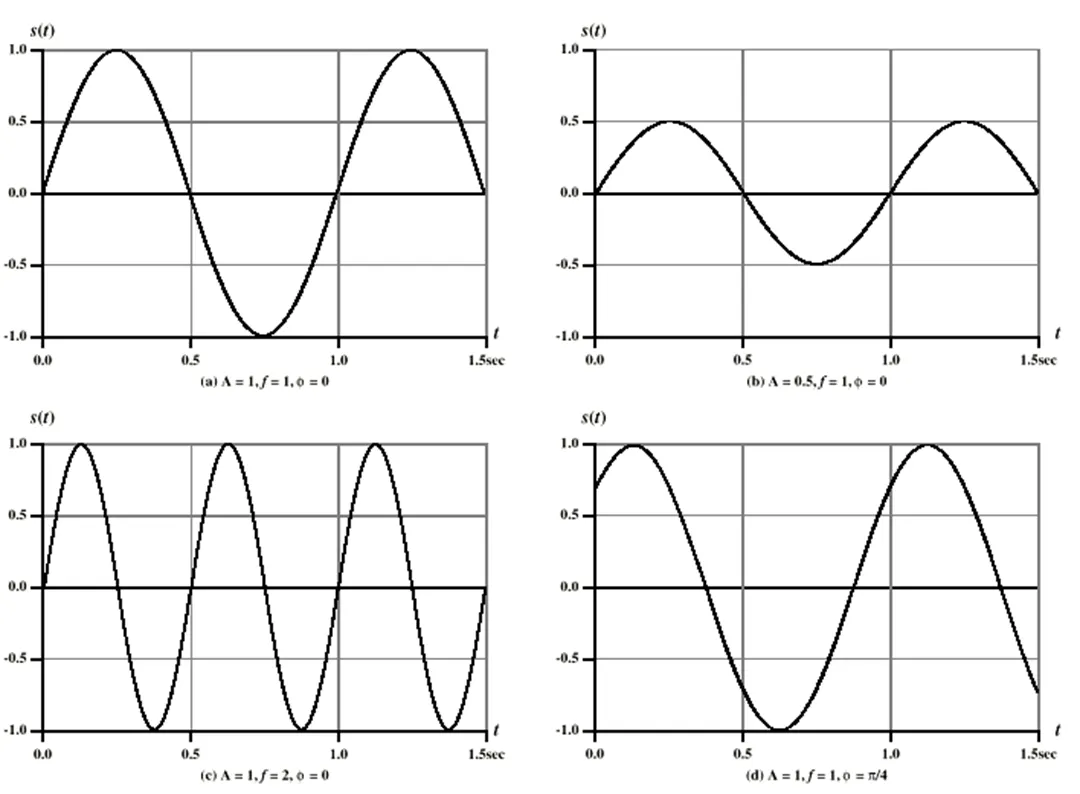
Peak Amplitude || 최대 진폭 (A)
◦
시그널의 Maximum-Strength(최대값)이며, 보통 전압(V)으로 표현된다.
•
Frequency || 주파수 (f)
◦
신호의 반복속도이다. 보통 헤르츠(Hz)로 표현되며, 신호가 보통 1초에 몇번 반복되는지를 나타내는데, T = 1/f로 표현할 수 있다.
•
Phase || 위상 (Φ)
◦
신호의 단일 주기 내에서 시간에 대한 상대적 위치 척도이다.
식으로 종합표현해보자. 이와 같은 형태를 Sinusoid(정현파)라고 한다.
두 신호 사이에는 시간적인 관계 뿐만 아니라 공간적인 관계 또한 존재한다.
신호 하나의 사이클이 차지하는 거리를 파장(λ)이라고 한다.
신호 전파속도를 v라고 할 때, 다음과 같은 식이 성립한다. 일반적으로 v는 광속(c)로 정의한다.
Frequency Domain Concepts || 주파수 영역 개념
전자기 신호는 많은 주파수로 구성가능하다.
두번째 주파수는 첫번째 주파수의 정수배이다. 이처럼 어떤 주파수와 기본적인 형태는 같으나 Strength, Phase등이 다른 경우 Primitive한 주파수를 Fundamental Frequency(기본 주파수), 해당 주파수의 정수배는 Harmonic Frequency(조화 주파수)라고 한다.
Fourier Analysis
푸리에 조합을 사용함으로써 모든 신호는 서로 다른 주파수의 정현파들의 합으로 구성됨을 알 ㅜㅅ 있다.
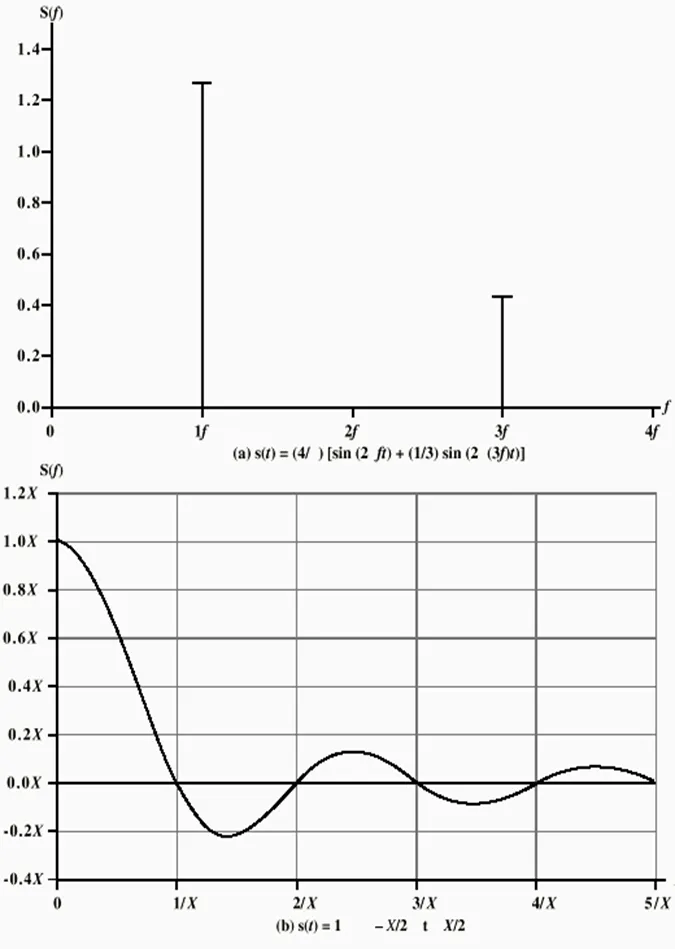
Spectrum & Bandwidth
•
Spectrum || 스펙트럼
◦
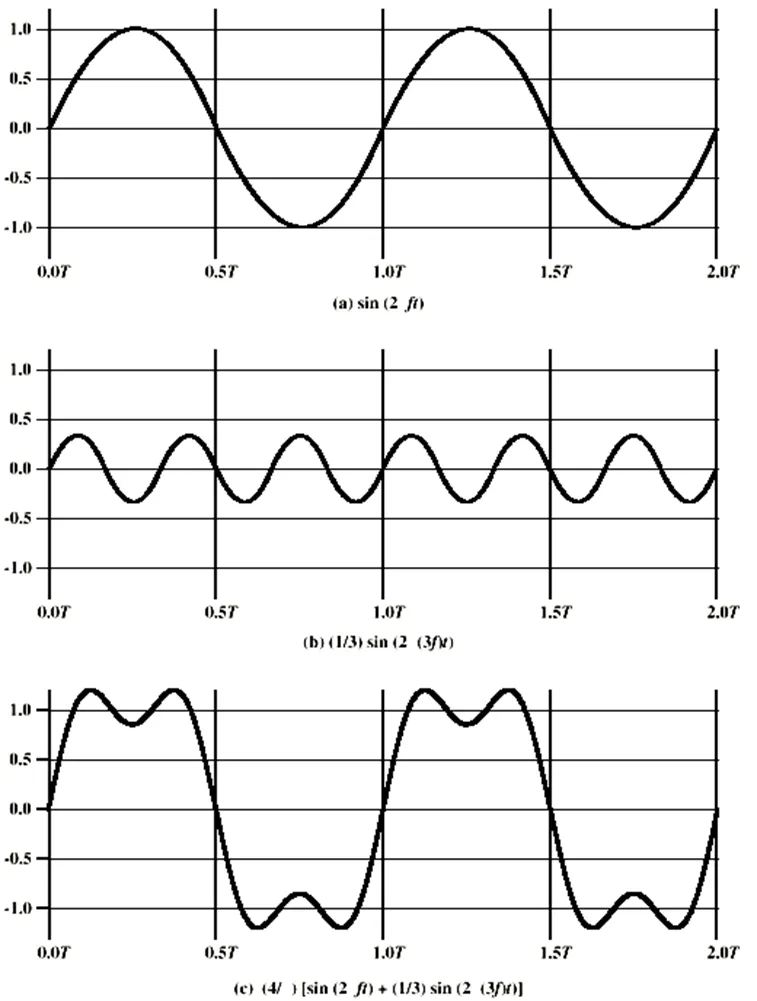
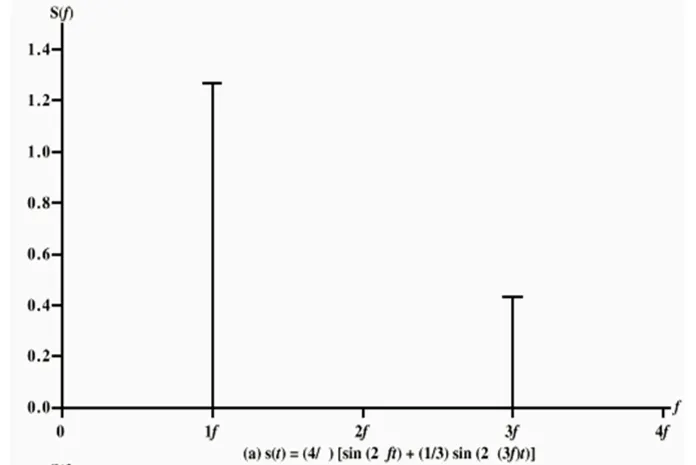
그 신호가 포함하는 주파수의 범위를 말한다. 윗 그림에서 신호는 f에서 3f까지 걸쳐져있다.
•
Absolute Bandwidth || 절대 대역폭
◦
스펙트럼의 폭을 의미한다. 즉, 해당 스펙트럼의 절대 대역폭은 2f이다.
•
Effective Bandwidth || 유효 대역폭 또는 대역폭
◦
상대적으로 좁은 영역에 주파수에 밀접되어 존재하는 곳의 대역폭
•
DC Component || 직류성분
◦
어떤 신호가 주파수 0의 성분을 가지고 있는 경우.
Data Rate and Bandwidth
유효 대역폭은 신호에너지 대부분이 집중되어있는 대역을 의미한다.
하지만, 이론적으로 무한한 대역의 주파수를 가지고 있다 하더라도, 실제 전송 시스템에서는 제한된 대역만을 허용한다.
전송매체에서 운반되는 데이터의 전송률을 제한하는 특성을 지닌다.
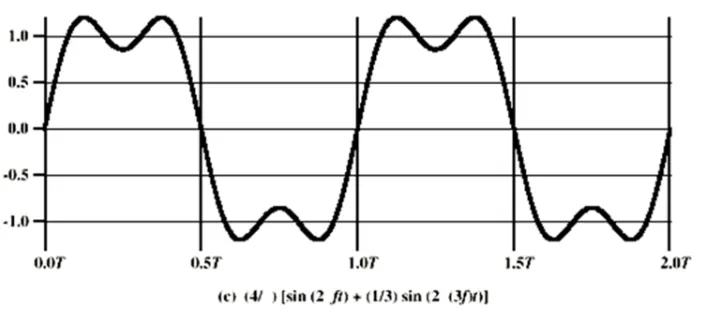
윗 그림을 생각해보자. 양 펄스는 0, 음 펄스는 1을 보낸다고 할 때, 예상되는 Binary Code는 0101…의 형태일 것이다. 각 펄스는 0.5f의 길이를 가질 것이므로, 데이터의 전송률은 2fpbs이 된다.
데이터 전송률은 초당 데이터가 얼마나 나가는가이므로, 각 데이터는 해당 데이터를 의미하는 펄스의 길이로 생각한다.
위 그림은 f에 3f의 사인파를 합쳐 원래의 방형파에 가까운 파형을 얻는다. 5f, 7f… 점점 많은 주파수를 더하는 과정을 계속한다면 원래의 방형파에 근사할 것이다. 즉 다음과 같은 식을 성립할 수 있다.
자세한건 푸리에 조합 참조.
아무튼 이로써 최대 Strength가 A인 방형파를 얻었다.
다만 앞서 말했듯이 실제 전송 시스템에서는 제한된 대역만을 허용하게 된다. 따라서 이론적으로 완벽한 푸리에조합 방형파는 실제 데이터 통신에서는 사용할 수 없다.
그러나 식을 잘 보라! k의 값이 클 수록 실제 저장되는 에너지의 값은 1/k밖에 되지 않는다. 즉, 낮은 주파수가 대부분의 에너지를 다 가지고 있기 때문에 낮은 주파수 위주로 보내게 된다면 어느정도 근사가 가능할 것이다!
다만, 대역폭을 제한하면 왜곡이 유발되며, 수신신호를 해석하는 작업이 훨씬 더 어려워진다. 제한하는 폭이 더 작을 수록 오류 발생률도 높아지므로 유의하자.
Analog and Digital Data Transmission
대략적으로, 아날로그는 연속적이고 디지털은 이산적이다.
•
Data : 정보(information)를 포함하는 개체
•
Signals : 데이터의 전자기적인 표현
•
Signaling : 물리적으로 매체를 통해 전파하는 행동
•
Transmission : 정보의 송수신과 가공을 하여 데이터를 주고받는 행위
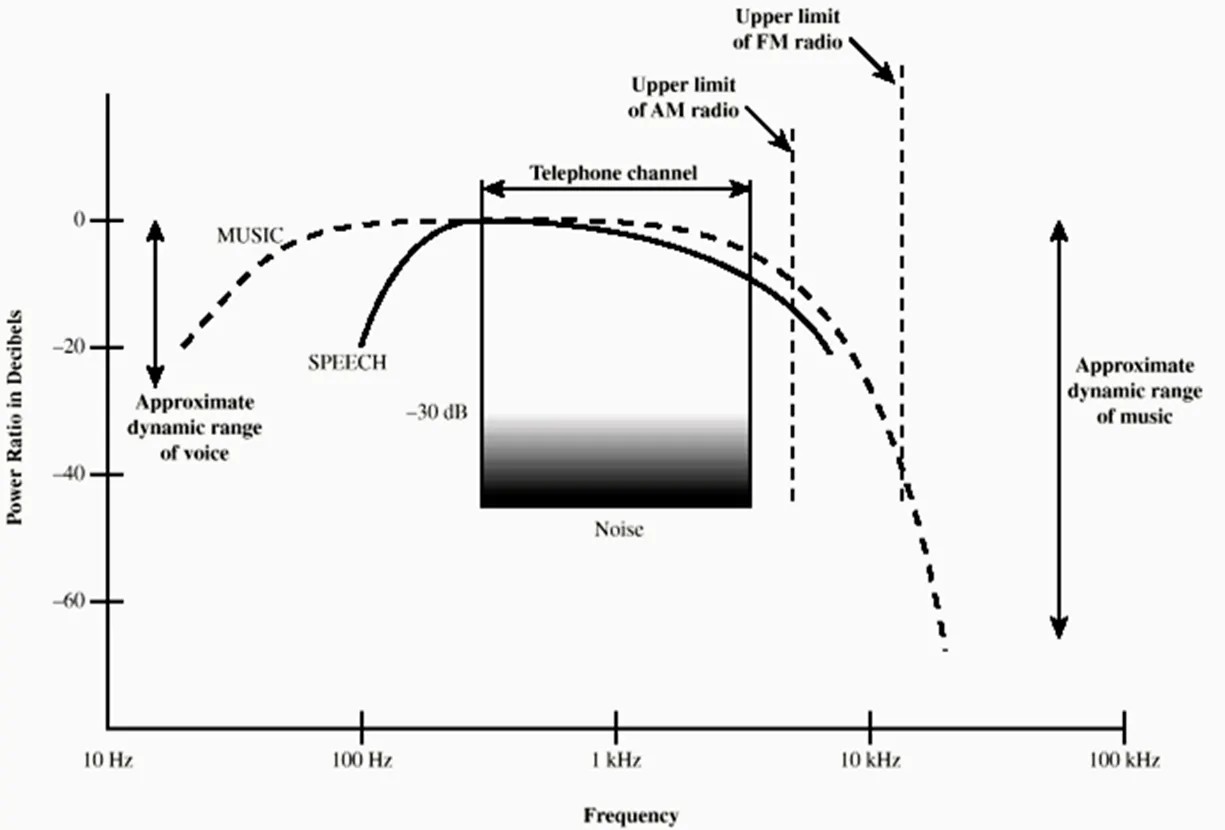
Acoustic Spectrum(Voice)
음악의 평균 주파수는 30Hz에서 30kHz까지 분포하며, 목소리의 경우는 일반적으로 100Hz에서 8Hz 정도까지 분포한다.
이때 Telephone Channel이 허용가능한 주파수는 500Hz~6kHz정도이므로, 해당 대역을 벗어나는 소리
미해결 사건부
만약에 인풋 시그널의 주파수가 채널이 허용가능한 주파수를 넘을 경우 1. 무시한다. 2. Channel 내에서 허용가능한 최대값으로 표현한다. 3. 기기의 설정에 따른다.
각 채널에서 최저 주파수 대역, 최고 주파수 대역을 설정하는 이유는?
Digital Data
디지털 신호가 가지는 장단점
장점 : 싸다. 노이즈 감지에 훨씬 민감하다.
단점 : 아날로그에 비해 감쇠현상이 심하다. 이를 위해서 중계기와 증폭기를 끼우는 작업을 해줘야한다.
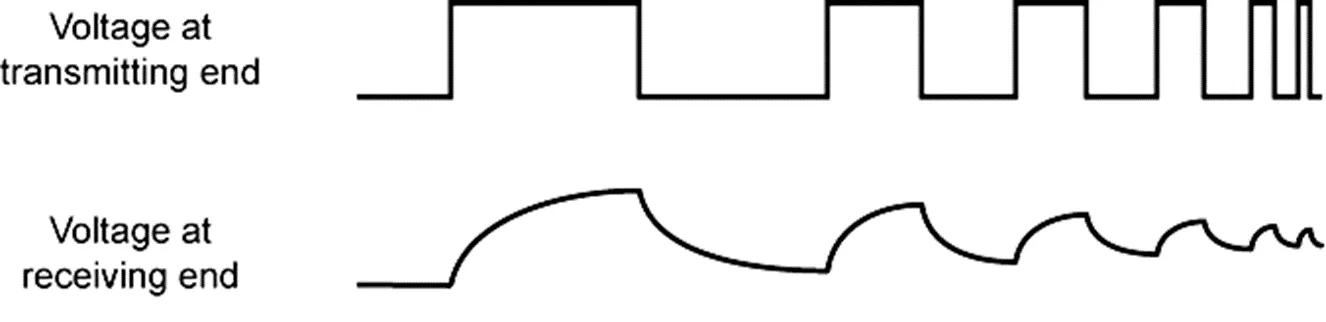
높은 주파수에서 신호 세기가 감쇄되므로 펄스들이 둥글어지고 작아진다.
강슬설
Audio Signals
오디오 정보 중 하나는 음성인데, 주파수의 범위가 20Hz~20kHZ이다.
전송을 위한 전자기파로는 쉽게 변환된다.
소란스러운 정도로 측정되는 소리 주파수는 전자기파의 주파수로 변환되고, 진폭은 전압으로 표현된다.
음성 데이터의 경우 원래의 음성과 동일한 스펙트럼을 갖는 전자기 신호로 직접 표현될 수 있다. 그러나 소리의 음질과 대역폭이 증가할 수록 전송 비용이 비싸지므로 둘 사이의 절충안이 필요하다.
오디오는 100~7k의 주파수에 해당하므로 오디오 신호로 변환하기 메우메우 쉽다.
전화 채널은 주파수 대역을 300~3400정도로 제한한다.
TV는 나중에 개발되어 전화채널과 비슷한 방식을 사용하나 더 높은 주파수를 사용한다.
강슬설
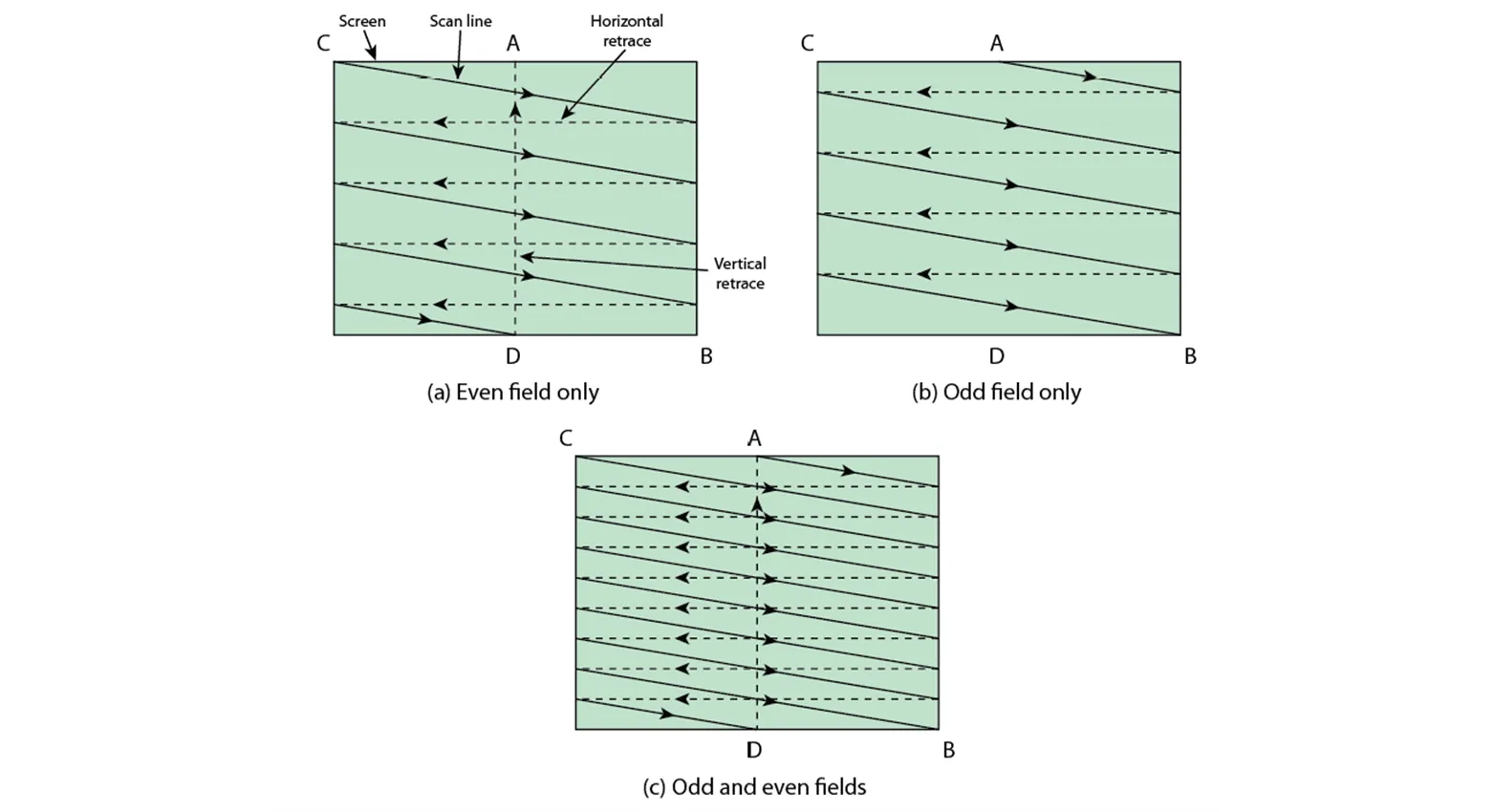
Video Signals
NTSC와 PAL
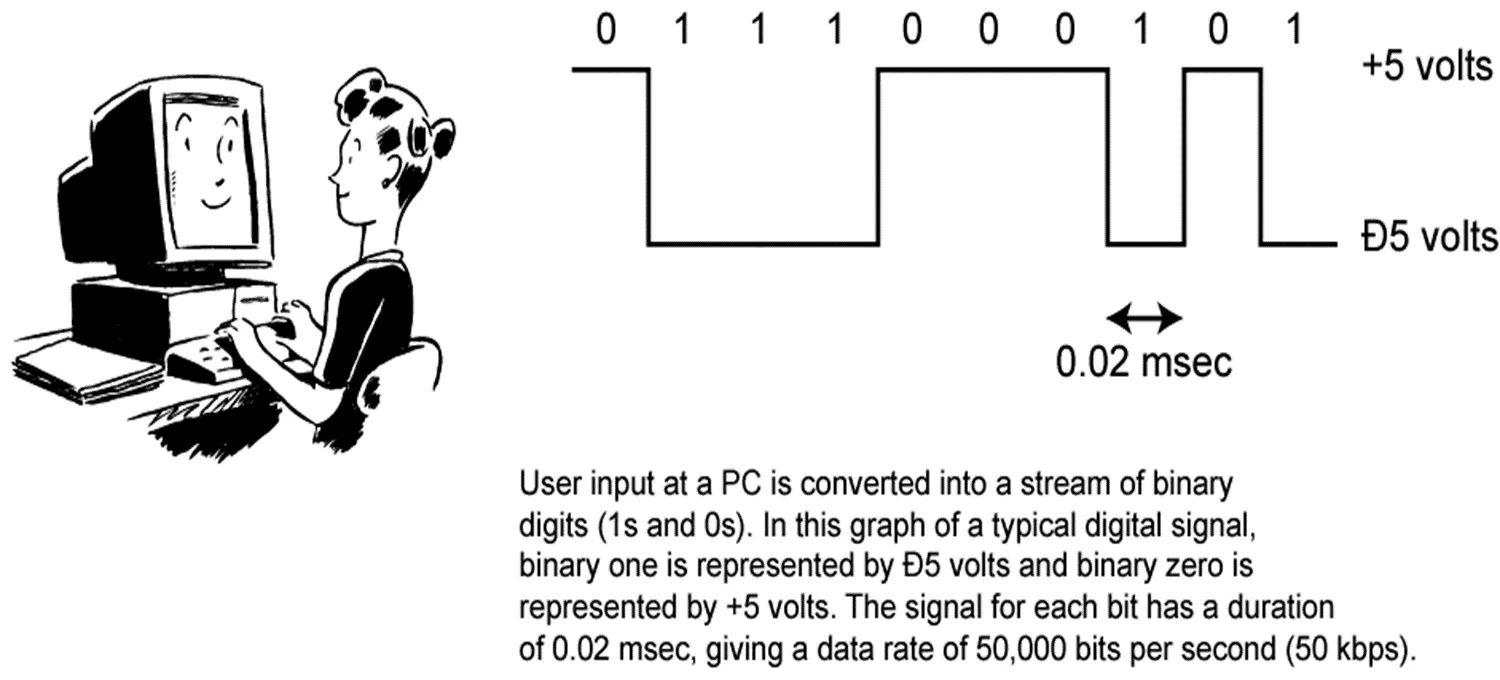
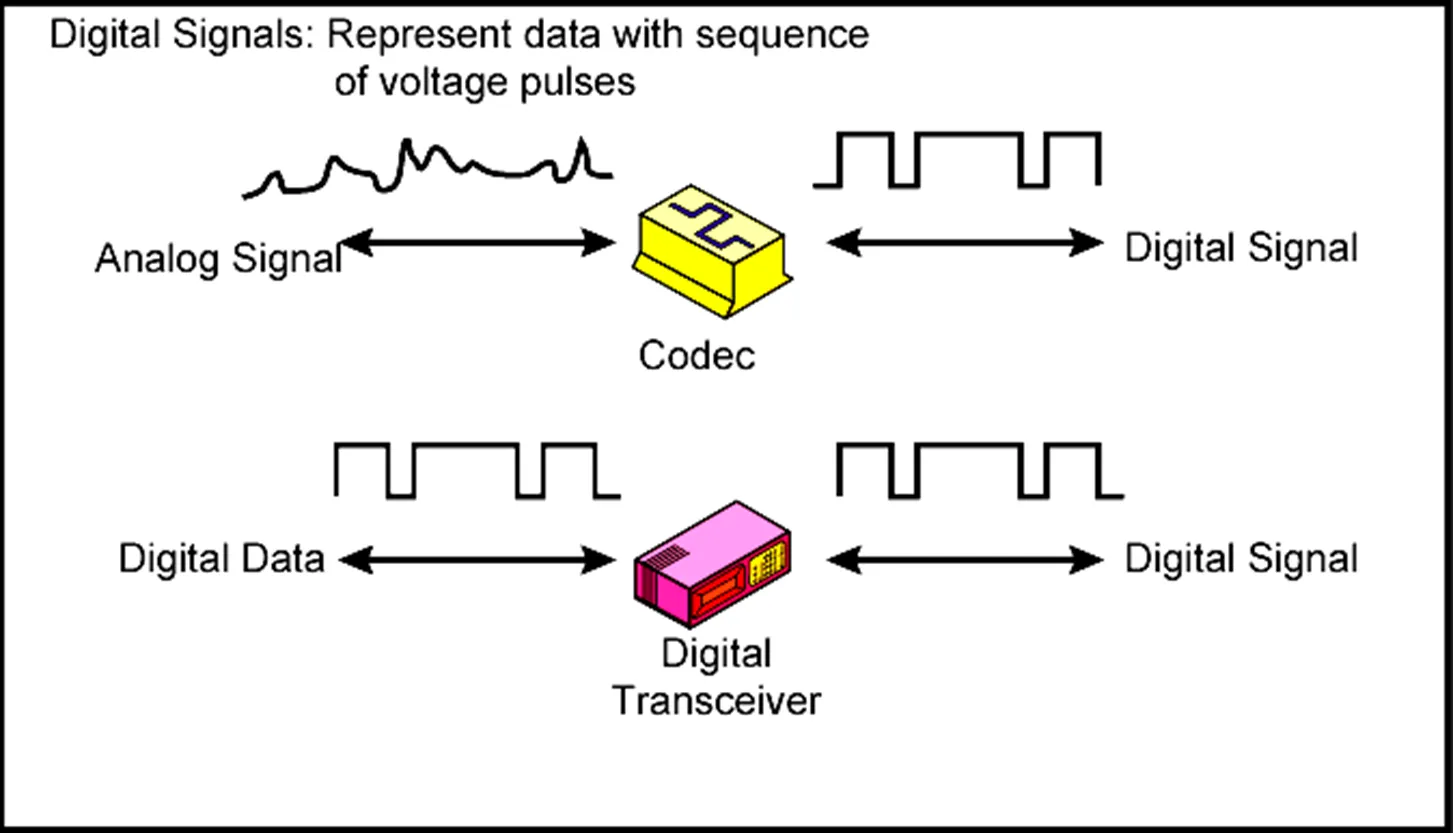
Conversion of PC Input to Digital Signal
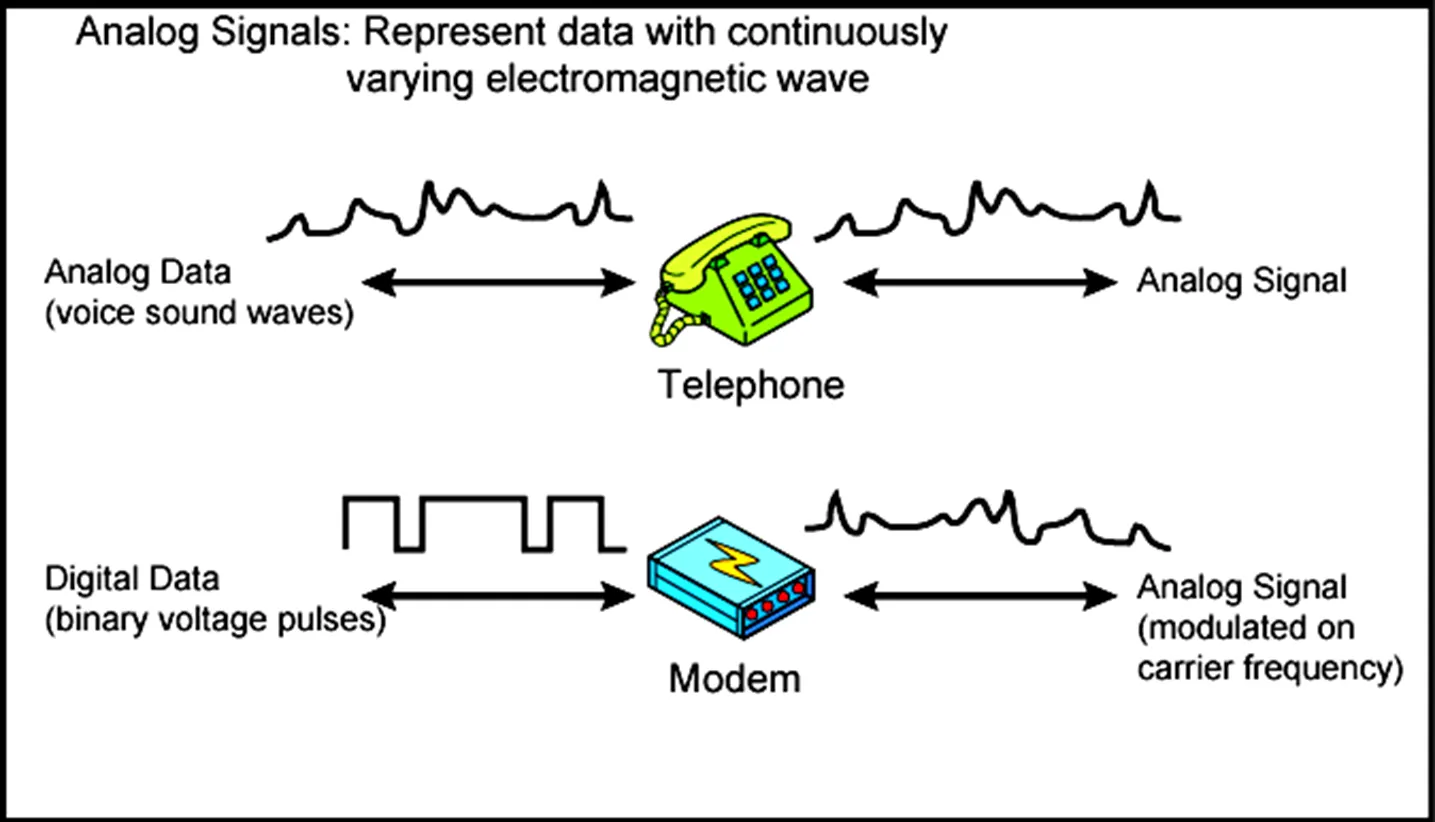
Analog Signals
Digital Signals
Transmission Impairment
받은 시그널이 모종의 이유로 형태가 변할 수 있다.
•
아날로그의 경우 시그널 퀄리티의 하락
•
디지털 : 비트 에러
가장 흔한 Impairments는
•
감쇠왜곡
◦
전송매체를 통과하는 거리에 따라 점점 신호가 약해지기 때문에 발생하는 현상이다.
•
지연왜곡
◦
신호전파의 속도가 주파수에 따라 다르기 때문에 발생하는 현상이다.
•
노이즈
◦
감쇠
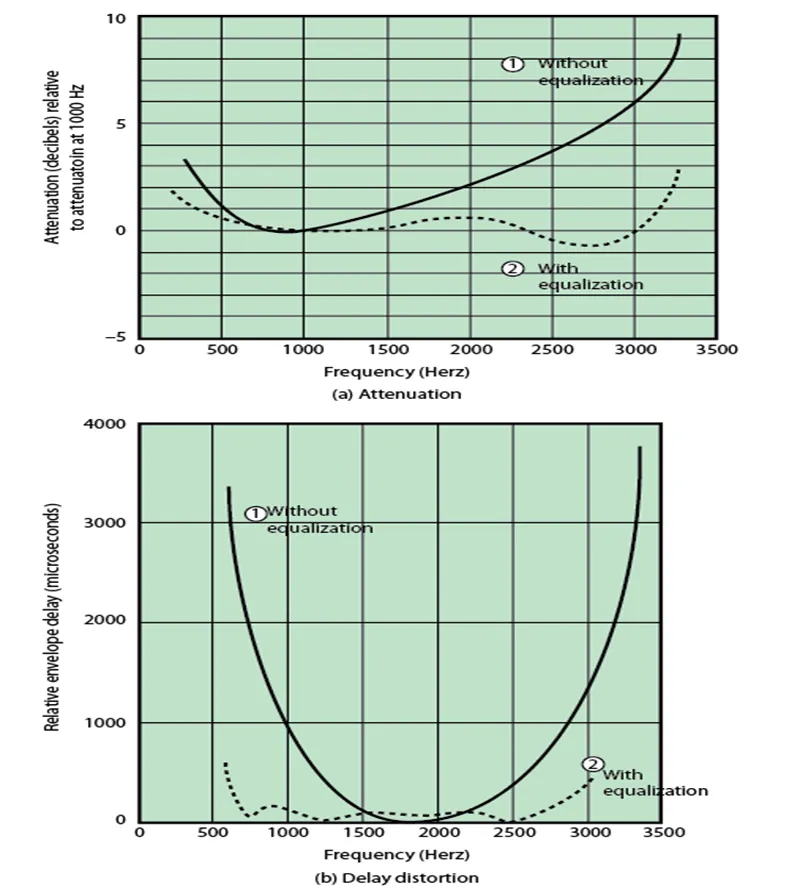
Attenuation Distortion
신호의 세기는 전송매체를 통과하는 거리에 따라 점저 약해진다.
•
Guided Transmission media의 경우
◦
지수적으로 이루어지므로, 단위 거리에 대한 일정 데시벨의 값으로 나타낸다.
•
UnGuided Transmission media의 경우
◦
감쇄는 거리와 대기 특성의 복잡한 함수로 표현된다. 감쇄현상에 대한 세 가지의 고려사항이 필요하다.
감쇄현상에 대해서 주의해야할 가장 큰 요소는 3가지다.
1.
수신 신호는 수신기의 전자회로가 신호를 인지하고 해독하기에 충분한 세기를 가져야한다.
2.
오류없이 수신이 가능할 정도로 신호는 잡음에 비해 충분히 큰 강도를 유지해야한다.
3.
감쇄는 주파수에 따라 변한다.
1,2번은 신호 세기의 감쇄와 관련된 문제이므로 증폭기나 리피터를 사용하여 문제를 해결한다.
Point 2 Point의 경우 송신기의 신호세기는 수신기가 인지하기에 충분히 커야하지만, 디바이스의 전자회로에 왜곡현상을 발생시킬 정도로 커서는 안된다.
특정 거리를 넘을 경우 감쇄현상이 매우 심해지므로, 일정 거리마다 증폭기와 리피터를 넣는것이 중요하다.
3번의 경우 매우매우매우 주의해야하는 문제다.
감쇄현상은 주파수의 함수이므로, 수신신호가 왜곡되며 인지도(intelligibility)가 떨어진다.
이 문제를 해결하기 위해서는 전체 주파수 대역에 걸쳐 감쇄 정도를 동일하게 해야 한다.
위 그래프는 1000Hz와 비교하여 HZ별로 얼마나 감쇄현상이 더 심한지를 알려준다.
식은 다음과 같다.
•
음성 대역폭의 상한 주파수는 저주파수보다 더 많은 감쇄를 받는다. 이는 명백하게 음성신호의 왜곡을 유발한다.
반대로 디지털 신호의 경우에는 감쇄왜곡현상이 문제가 심각하지 않다. 디지털 신호의 세기는 주파수가 증가함에 따라 감소하기 때문이다.
Delay Distortion
지연 왜곡은 유도 전송매체에서 신호전파 속도가 주파수에 따라 다르기 때문에 발생한다.
Band limited(제한적 대역)신호의 경우에는 중간 주파수에서 속도가 가장 빠르고, 양쪽 끝으로 갈 수록 속도가 감소한다.
따라서 한 신호의 여러 주파수 성분들은 각각 다른 시간에 수신기에 도착하게 되고 그 결과 다른 주파수들간의 편이가 나타난다.
지연왜곡은 아날로그보다 디지털 신호일때가 영향이 더 크다.
지연왜곡으로 인해 하나의 비트위치에 해당하는 신호성분이 다른 비트와 겹치게 되어 intersymbol interference를 유발시키는데, 전송채널의 최대 전송속도를 제한하는 주요한 요인이 된다.
강슬설
Noise
감쇠왜곡이나 지연왜곡은 전송 시스템에 의해 일어나는 일이지만, 노이즈의 경우 데이터를 전송하는 과정에서 불필요한 신호가 추가되는 것이다.
잡음은 네가지 유형으로 분류된다.
•
Thermal Noise(열잡음)
•
Intermodulation Noise(상호변조잡음)
•
Crosstalk(누화)
•
Impulse Noise(충격잡음)
Thermal Noise || 열잡음
전자의 열 교란으로 인해 생기는 잡음을 열잡음이라 한다.
모든 장치와 전송매체에서 발생하며 온도의 함수이다.
통신 시스템이 사용하는 전체 주파수 대역에 걸쳐서 고르게 분포된다.
열잡음은 제거될 수 없기 때문에 통신 시스템 성능의 상한선으로 작용한다.
이거 열잡음 구하는 거 시험에 나오나?
Intermodulation Noise || 상호변조잡음
서로 다른 주파수의 신호가 동일한 전송매체를 공유할 때 생기는 현상
주파수 4000Hz와 8000Hz가 동일한 Transmission Medium을 공유할 때, 12000Hz의 에너지가 생성되며 원래 12000Hz의 주파수를 가진 신호에 대한 간섭으로 작용한다.
Crosstalk || 누화
신호의 경로가 비정상적으로 결합된 경우에 발생하는 현상
Impulse Noise || 충격잡음
외부적인 전자기적 충격이나 통신 시스템에서의 결함으로 인해 발생하는 현상
Channel Capacity
주어진 통신선로 혹은 채널상으로 전송할 수 있는 최대 전송률을 채널 용량이라 한다.
•
Data Rate || 데이터 전송률 : 데이터의 통신 속도로서 단위는 초당 비트수이다.
•
Bandwidth || 대역폭 : 송신기와 전송매체의 특성에 의해 제한되는 전송 신호의 대역폭으로 단위는 초당 사이클, Hz이다.
•
Noise || 잡음 : 통신선로상에서 잡음의 평균레벨이다.
•
Error Rate || 오류율 : 오류 발생비율이다.
통신설비가 가뜩이나 비싼데, 설비가 지원해야하는 대역폭이 클 수록 비용도 높아진다.
전송매체의 물리적인 특성과 다른 발신지와의 간섭 방지를 위해서도 제한이 생기게 된다.
그러므로 주어진 대역폭을 가능한 효율적으로 사용해야한다.
Nyquist Bandwidth
대역폭이 B일 경우 전송가능한 최대 신호율은 2B이다
•
지연왜곡에 의해 유발되는 Symbol간 간섭의 효과로부터 도출된다.
디지털-아날로그 인코딩 기법의 개발에 유용하다.
여기에서 M은 전압레벨, 혹은 이산적 신호의 수를 나타낸다.
따라서 주어진 대역폭에서 서로 다른 신호 요소의 수를 증가시키면 데이터 전송률이 증가한다.
수신기의 부담 또한 증가시킨다. 각 신호시간동안 M개의 신호중에 하나를 구분해야하기 때문
전송선로상의 잡음과 기타 손상이 M의 실제 값을 제한다.
Shannon Capacity Formula
Nyquist는 다른건 다 제쳐두고 자연왜곡의 경우 대역폭을 2배로 증가시키면 데이터율이 2배가 된다는 걸 보여줬다. 그러나 문제가 그것뿐이겠는가? 나머지 요소를 곱연산 할 시간이다.
잡음은 하나 이상의 비트를 손상시킨다. 데이터 전송률이 더 짧아질 수록, Bandwidth가 커지므로 비트는 짧아지고 더 많은 비트가 손상된다.
주어진 노이즈 레벨에서 신호의 세기를 크게 하면 데이터를 보다 정확하게 수신할 수 있는데, 이런 관점에서 바라본 파라미터가 바로 SNR(Signal Noise Ratio)이다.
이러한 SNR 값은 신호를 처리하고 데이터를 복원하는 수신측에서 측정된다.
SNR은 잡음값을 초과하는 정도를 데시벨로 나타낸다는 의미인데, 높은SNR값은 양질의 신호를 의미하며 적은 수의 리피터를 요구한다.
따라서 SNR이 데이터 전송률의 상한선을 결정하게 되므로 데이터의 전송에서 중요한 의미를 가진다.
최종 전송률은 다음과 같다.
Next chapter