Previous chapter
Combine Schemas?
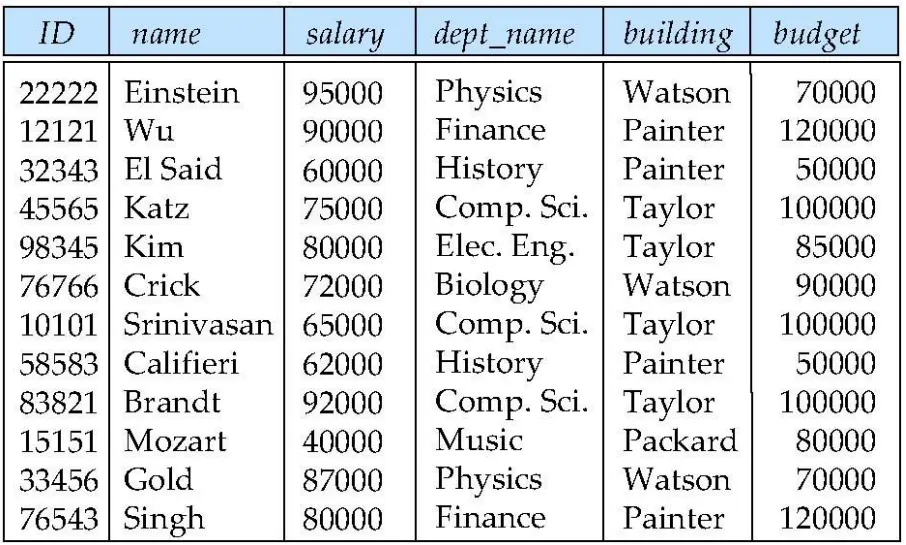
instructor와 department를 inst_dept로 합친다고 가정하자.
•
inst_dept에 Connection은 존재하지 않는다고 하자.
두 Relation을 합쳐놨을때 데이터가 중복이 되는 것을 확인할 수 있다.
Attribute의 개수가 늘어날 수록 데이터가 차지하는 공간이 늘어날 수 있다.
A Combined schemas without Repetition
•
set_class(sec_id, building, room_number)
•
section(course_id, sec_id, semester, year)
를 다음과 같이 합친다고 하자.
•
section(course_id, sec_id, semester, year, building, room_number)
이 경우에는 데이터에 대한 중복이 없을 것이다.
이런 것들을 보다 규칙적으로 구분할 수 있도록 규칙에 대해 알아보자.
What About Smaller Schemas?
inst_dept를 다시 생각해보자.
이 테이블 자체가 가장 컴팩트한 단위인가?
instructor : ID에 따라 → name, salary, dept_name이 결정된다.
department : dept_name에 따라 → building과 budget이 결정된다.
attribute간에 어떤 function dependency가 있는지 확인하라.
•
functional dependency: dept_name → building, budget
◦
여기에서 dept_name이 candidate key가 된다.
inst_dept에서 dept_name이 candidate key는 아님. 하지만 building과 budget은 dept_name에 의존함.
즉, building과 budget은 반복될 수 밖에 없음 → decompose가 더 나을 것.
하지만 쪼개는 것도 잘 해야한다.
다음과 같은 예시를 보자.
•
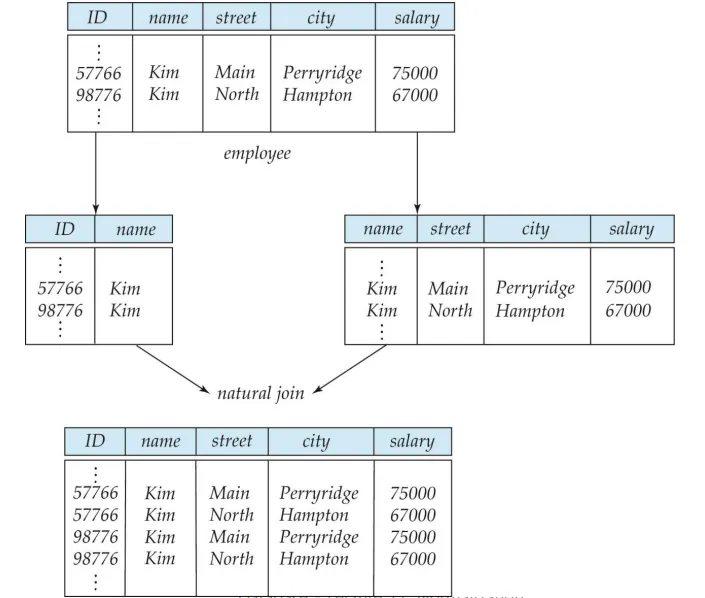
employee(ID,name, street, city, salary)를
•
employee1(ID,name)
•
employee2(name, street, city, salary)
이름이 같은 사람의 경우를 생각하지 않았으므로, 데이터의 손실이 일어날 수 있다.
원래는 1대1 대응이 될 의도였으나 Natural Join을 하면서 필요없는 데이터가 추가로 생겼을 뿐만 아니라 ID도 Primary Key로써의 역할을 잃게되는 대참사가 일어난다.
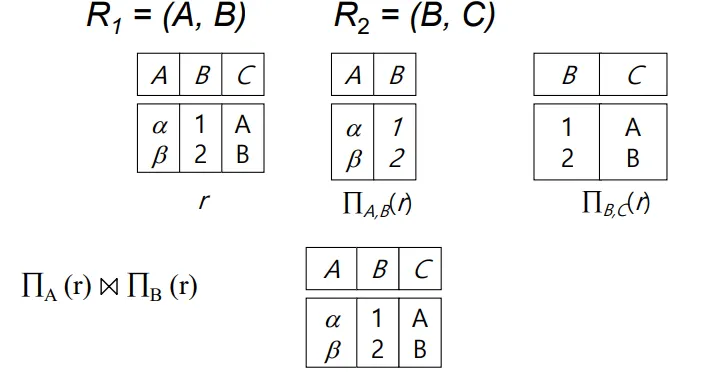
Example of Lossless-Join Decomposition
Decomposition of
B가 공통 attribute일 경우 재결합을 했을때 손실되는 데이터가 없으므로, Lossless Decomposition이라고 할수 있다.
First Normal Form
값들이 나눌 수 없다면 그 도메인은 반드시 아토믹 해야한다.
relation schema R의 모든 attribute가 atom ic할 경우, R을 first normal form이라고 정의한다.
Goal — Devise a Theory for the Following
Relation이
중복된 데이터 최소화 but 필요한 데이터는 모두 갖게!
functional dependencies
multivalued dependencies
Functional Dependencies
R을 relation schema라고 가정하자.
functional dependency는 다음과 같다.
Examples
a에 1을 넣으면 4가 될 수도 있고 5가 될 수도 있다. 따라서 가 될 수 없다.
b에 각 값을 넣을 때 2개 이상의 값이 나오지 않으므로 이다.
Functional Dependency는 notion of key의 일반화 버전
inst_dept(ID,name, salary, dept_name, building, budget)
dept_name → building
ID → building
dept_name → salary
functional dependency에서는 특이한 경우가 몇가지 존재한다.
•
name →name
Closure of a Set of Functional Dependencies
Properties of Functional Dependencies
•
Subset Property : Y가 X의 부분집합일 경우 X→Y
•
augmentation : X→Y일 때, XZ→YZ이다.
◦
똑같은 Key Z를 추가해도 XZ는 YZ를 결정한다.
•
Transitivity : X→Y이고 Y→Z일 때, X→Z이다.
•
Union : X→Y이고, X→Z일 때 X→YZ이다.
•
Decomposition : X →YZ일때, X→Y이고, X→Z이다.
•
Psudo-transitivity : X→Y이고 WY→Z일때 WX→Z이다.
Boyce-Codd Normal Form
BCNF는 다음 조건 중 하나라도 만족하면 성립할 수 있다.
•
a→b 가 trivial 하다()
•
a가 R의 슈퍼키다.
Example not in BCNF
instr_dept(ID, name, salary, dept_name, building, budget)
Assembly
복사
ID → name, salary, dept_name, building, budget
ID는 모든 attribute에 FD하므로 superkey 또는 candidate key가 될 수 있다.
dept_name → building, budget
dept_name은 building과 budget만 정할 수 있으므로 현재 주어진 superkey가 아니다.
building, budget이 b이고 dept_name가 a일 경우, b가 a의 부분집합이 될 수 없다.
따라서 dept_name은 BCNF가 될 수 없다.
Decomposing a Schema into BCNF
관계 R을 다음과 같이 나누자.
•
•
•
우리의 예제에서 a = dept_name, b= (building, budget)
Decomposition Examples
HR(DPT_NO, MGR_NO, EMP_NO, EMP_NAME, PHONE)
F = DPT_NO → MGR_NO
DPT_NO → PHONE
EMP_NO → EMP_NAME
이때 DPT_NO → MGR_NO가 될 수 없다.
Decomposition
•
HR1(DPT_NO, MGR_NO) ==
•
HR2(DPT_NO, EMP_NO, EMP_NAME, PHONE) ==
끝? HR2를 잘 보라.
여전히 DPT_NO → PHONE이 남아있으면서도, DPT_NO가 슈퍼키가 아니므로 BCNF Violation이 일어난다.
BCNF can decompose "too much”
BCNF가 안나눠질때까지 나누면 되는 문제인가?
ex) AB → C && C → B?
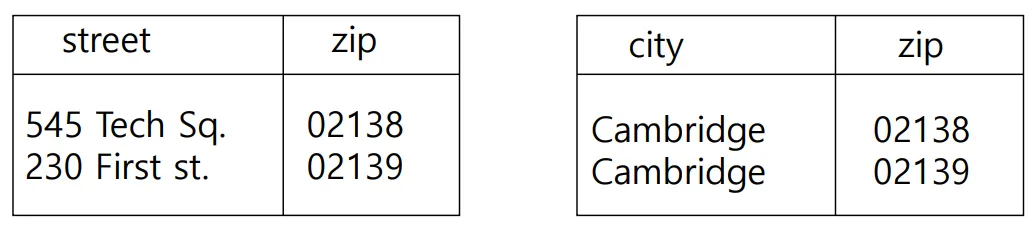
A = street, B = city, C = zip
AB → C :
C → B : FD가 성립된다.
zip이 superkey가 될 수 있는가? → 아니다.
그럼 Decomp.
•
BC, AC
An Unenforceable FD
BCNF가 FD를 고려하지 않고 너무 잘게 쪼개기 때문에 FD가 쪼개지는 현상이 발생하게 된다.
BCNF는 너무 엄격하고 너무 잘개 쪼갠다는 문제가 있다.
Third Normal Form: Motivation
3NF는 다음 조건 중 하나라도 만족하면 성립할 수 있다.
•
a→b 가 trivial 하다()
•
a가 R의 슈퍼키다.
•
b-a에 있는 각 attribue A가 candidate키의 일부인 경우 3NF를 만족한다.
내용에서 알 수 있다시피 BCNF를 만족하면 반드시 3NF를 만족하게 되는 방식이다.
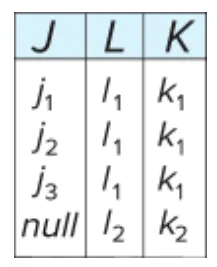
Redundancy in 3NF
•
R = (J, K, L )
•
F = {JK → L, L → K }
JK → L, L→K
(b-a) 가 candidate key에 들어가는가?
city가 candidate가 될 수 있으므로 3NF에 해당한다!
몇가지 문제가 생김
•
3NF는 FD를 지키는 성격이 있어서 정보의 중복이 생길 수 있다.
•
때때로는 Null Value가 포함될 수 있다.
Comparison of BCNF and 3NF
3NF가 BCNF에 비해 지니는 장점은 다음과 같다.
•
FD를 보존한다.
3NF의 단점
•
중복 정보와 null value를 사용하게 되어 스페이스의 낭비
Goals of Normalization
•
데이터베이스를Normalize하는 이유
◦
적은 저장공간
◦
빠른 없데이트
◦
데이터 일관성 유지
◦
명확한 관게
◦
새로 데이터 추가가 쉬움
◦
유기적인 구조
Design Goals
DB 디자인의 골은
•
가능하면 BCNF를 지키자.
•
Lossless join
•
Dependency 보존
모두 달성할 수 없다면
•
Dependency 보존을 포기하던가
•
3NF를 사용하는 방법으로 대체하라.
Functional-Dependency Theory
중요X
Closure of a Set of Functional Dependencies
•
if (reflexivity)
• if a → b, then ra → rb (augmentation)
• if a → b, and b → r, then a → r (transitivity)
Examples
R = (A, B, C, G, H, I)
F = { A→B
A→C
CG→H
CG→I
B→H}
Dependency Preservation
Fourth Normal Form
교과서 보시오…
Next chapter