Search

Projection

course
last review
mastery
none
progress
not started
date
2023/04/27
4 more properties
Previous chapter

Today’s MAIN QUEST

3차원 효과를 위해 꼭 필요한 요소 3가지
1.
앞에 있는 것이 뒤에 있는 것을 가릴 것
a.
Hidden Surface Removal, Depth Buffer
2.
빛과 그림자
a.
튀어나오고 들어간 곳이 입체처럼 느껴지도록
3.
원근 투영
a.
멀리 있는 건 작게 가까이 있는건 크게
b.
그와 동시에 생기는 소실점

BASICS

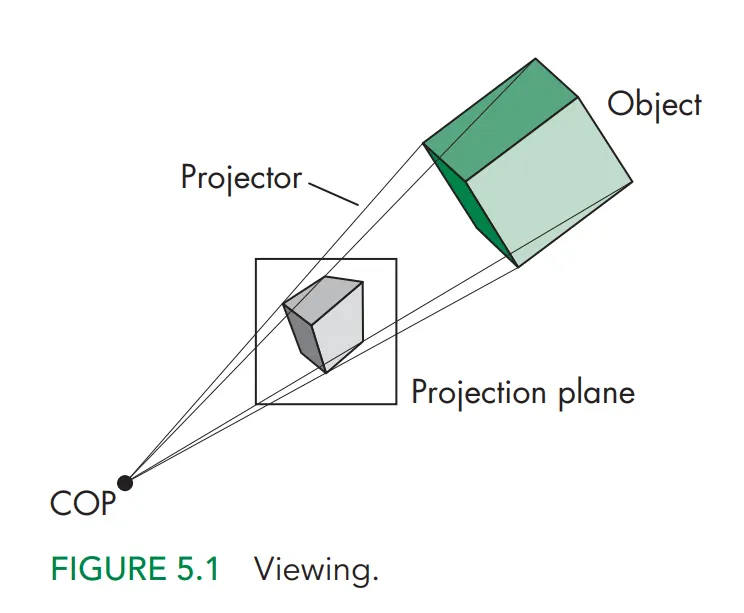
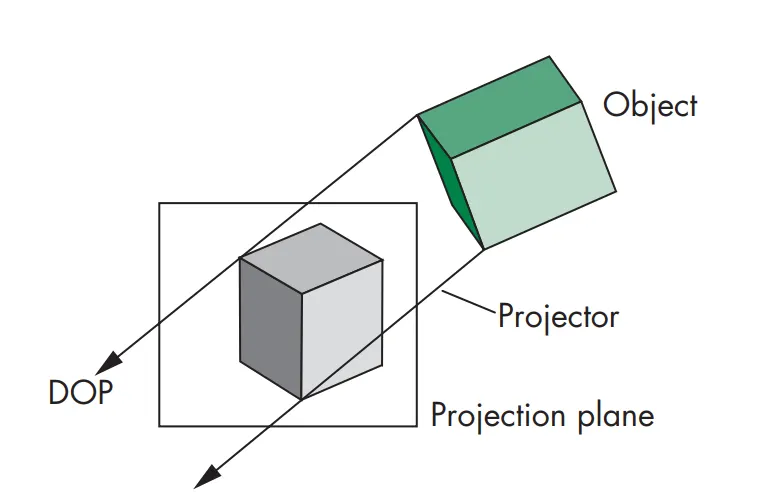
먼저 기본적으로 카메라에 상이 맺히는 평면 공간이 필요할 것이다. 이를 Projection Plane(View Plane)이고 한다. 투영선들은 투영 중심(Center of Projection)에서 만난다. COP는 카메라 렌즈의 중심, 즉 카메라 프레임의 원점에 해당한다. 이때 COP의 거리를 무한대로 멀리 보내버리자. 투영선의 각도가 점점 평행해지고 따라서 COP는 투영방향(Direction of Projection)으로 바뀐다.
•
COP가 무한대로 떨어지게 되더라도 투영면은 고정되고 영상의 크기는 항상 같게 유지된다.
따라서 COP가 유한한 상태일 경우를 Perspective Views(투시 관측), 무한할 경우를 Parallel Views(평행관측)라고 한다.

Parallel Views

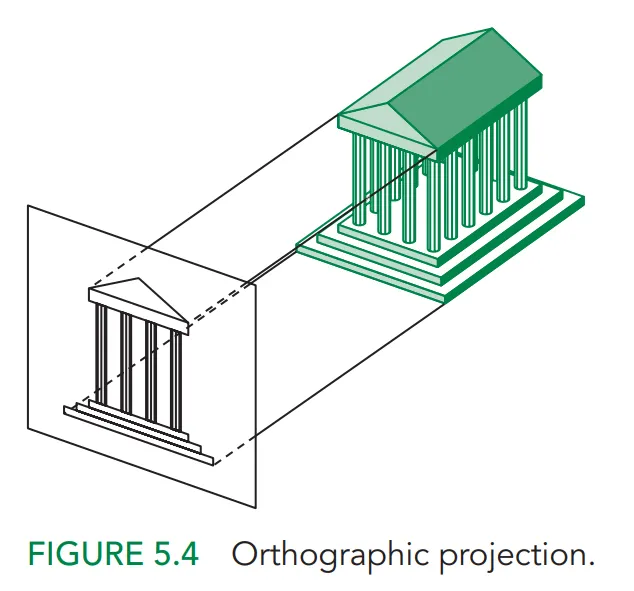
Orthogonal Projection

직교투영은 투영선이 투영면에 수직인 투영방식을 뜻한다.
AXIS PLANE
•
XY : 정면도
•
YZ : 측면도
•
XZ : 입면도
다시점 직교투영에는 여러개의 투영면이 존재하며, 각각의 투영은 오브젝트의 주면중 하나와 평행한 투영면이 존재하는 방식이다.
직교투영은 투영선이 관측 면에 수직인 평행투영의 특별한 경우이다. 만약 투영선이 XY평면에 평행하고, Z축에 직교하고 있을 때의 투영방정식은 다음과 같다.
P(xp,yp,zp)=(x,y,0)P(x_p,y_p,z_p) = (x,y,0)
[xpypzp1]=[1000010000000001][xyz1]\begin{bmatrix} x_p\\ y_p\\ z_p\\ 1 \end{bmatrix} = \begin{bmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&0&0 \\ 0&0&0&1 \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}
조금 더 일반적인 Orthogonal Projection을 만들기 위해 다음과 같은 식을 쓸 수 있다.
q=Mlpp=[xyz1],M=[1000010000000001]q = Mlp\\ p = \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} , M = \begin{bmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&0&0 \\ 0&0&0&1 \end{bmatrix}
M으로 표현된 투영행렬은 Vertex Shader을 수행한 후 하드웨어단계에서 실행된다.

ISOMETRIC PROJECTION

DOP : (1,1,1)
P=uuTPx=P(x∥+x⊥)=uuTx∥+uuTx⊥=uuT(ku)+u(uTx⊥=0)=ku=x∥\begin{align*} P &= uu^T\\ Px &= P(x_\parallel+x_\perp)\\ &= uu^Tx_\parallel+uu^Tx_\perp\\ &= uu^T(ku)+u(u^Tx_\perp = 0)\\ &= ku = x_\parallel \end{align*}
우리가 보는 방향벡터로 우리 화면에다가 끌고 오는 방식
방향 벡터에 align된 직육면체 내부의 것이 그려지게 된다.

Oblique Parallel

orthogonal : 직교투영을 하게 되면 거리는 일정함. 어느 방향에서든 거리 비율이 맞춰짐.
Oblique : 길이의 왜곡이 생기게 됨.

Perspective Views

원근 투영 변환(Perspective Projection Transformation)이란 우리 눈이 바라보는 방식으로 가상 공간을 변환하는 것이다. 가상 공간에서 눈에 대응하는 물체는 카메라이다.
원근 투영 변환을 설계하기 위해서는 눈에 보이는 범위를 카메라에도 설정해야하는데 이를 Field of View라고 한다.
카메라에 FOV를 설정하면 좌우와 위아래가 균등한 사각뿔의 영역이 만들어지게 된다.
원근 투영 변환은 x,y,z축이 모두 직교하는 정육면체 형태를 가진 뷰 공간을 카메라의 한 점으로 모이는 사각뿔 형태를 가진 공간으로 변환하는 작업이라고 할 수 있다.
3차원 공간을 변홚나 후에는 공간의 물체를 투영해 2차원의 모니터 평면에 담아내야 한다.
이를 위해 모든 물체의 상이 맺히는 가상평면을 생성하는데, 이를 Projection Plane이라고 한다.
•
Pojection Plane이 카메라(COP)로부터 멀어질 수록 Projection Plane은 더 커진다.
•
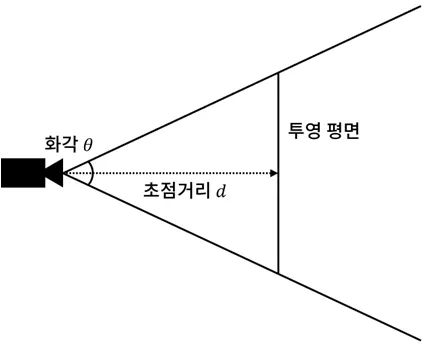
Projection Plane으로부터 COP까지의 거리를 초점 거리(Focal Length)라고 한다.
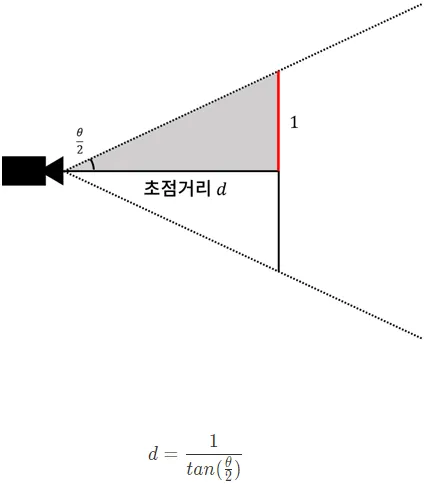
원근 투영을 계산하기 위해서는 먼저 투영평면의 위치를 지정해야한다.
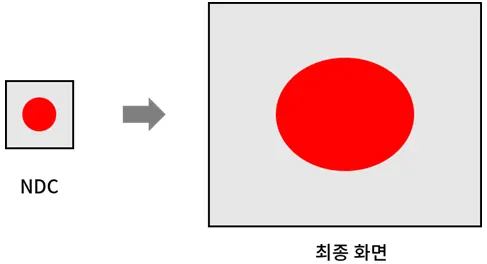
투영평면의 일반적인 위치는 계산의 편의를 위해 위아래의 크기가 각각 1이 되는 지점으로 결정한다. 좌우와 상하의 화각이 동일하므로, 투영 평면은 아래와 같이 좌우와 상하가 각각[-1,1]의 범위를 가지는 정사각형의 모습을 띄며 이 평면에 물체의 상이 맺히게 된다. 이 투영평면에 대응하는 정사각형 영역이 바로 NDC(Normalized Device Coordinate)다.
투영 평면에 대응하는 NDC가 언제나 일정한 값을 가져야 한다면, 카메라에 설정된 화각이 변할 때 초점거리가 달라지게 될 수 밖에 없다. 화각이 커지면 초점거리는 줄어들고, 화각이 작아지면 초점거리가 늘어난다. 둘 사이의 관계는 다음과 같은 수식으로 설정될 수 있다.
tan⁡(θ2)=1d\tan\left(\cfrac{\theta}{2}\right)=\cfrac{1}{d}
초점 거리가 구해졌다면, 뷰 공간의 점을 투영 평면 위의 점으로 대응시키는 Perspective Projection Transformation을 설계하자. PPT를 행렬로 표현할 수 있다면, 행렬 곱의 장점을 활용해 로컬 공간의 점을 투영 평면의 점으로 한번에 변환하는 파이프라인 제작이 가능할 것이다.
지금까지 진행한 공간 변환은 모두 x,y,z축이 서로 직교하고 크기가 동일한 정육면체 형태의 3차원 공간이었다. 이렇게 세 축이 모두 직교하는 공간을 유클리드 공간이라고 한다. 그런데 원근 투영 변환에 의해 정육면체 형태의 유클리드 공간이 사각뿔 형태로 바뀌게 되는데, 이를 사영 공간(Projective Space)이라고 한다.
사영 공간의 x축과 y축은 여전히 직교하나, 사영공간의 z축은 독립적이지 않고 x,y축에 종속적인 요소가 된다.
그렇다면 원근 투영 변환에 대응하는 행렬은 어떻게 설계하는게 좋을까?
유클리드 공간이 사영공간으로 변환되면서 x,y,z축이 모두 직교하는 체계가 달라지므로 원근 투영 변환에 대응하는 행렬은 지금까지 사용한 표준기저벡터의 변화를 관찰하는 방법으로는 생성할 수 없다. 문제를 단순화하기 위해 x축은 배제한 채로 이 문제를 해결해보자.
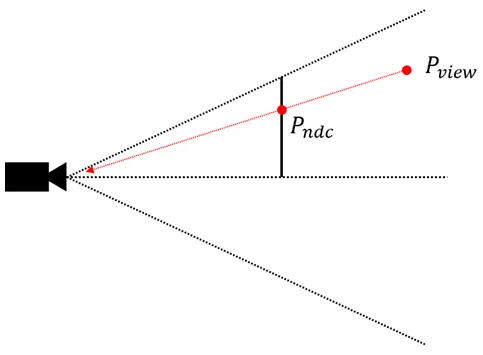
뷰 공간의 점 PviewP_{view}가 투영 평면에 투영된 점을 PndcP_{ndc}라고 할때 투영과정은 위와 같이 진행된다.
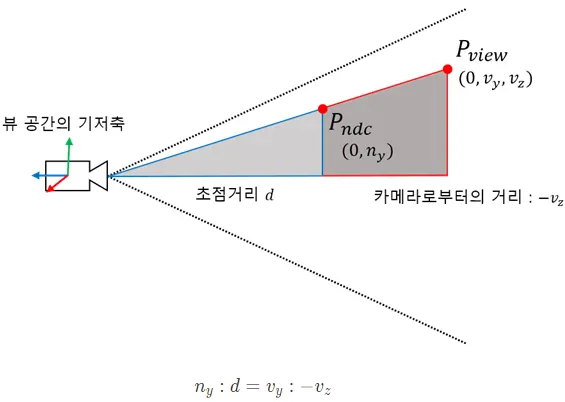
뷰 공간의 점 PviewP_{view}가 투영 평면에 투영된 점 PndcP_{ndc}의 좌표를 구하자. 쉽게 구해질 수 있다.
Pview=(vx,vy,vz),Pndc=(nx,ny,0)P_{view} = (v_x,v_y,v_z), P_{ndc}=(n_x,n_y,0)
뷰 공간에서의 카메라 앞에 위치한 점의 z값은 항상 음수이므로, 큰 삼각형의 밑변의 길이는 −vz-v_z가 된다. 즉 다음 식이 성립된다.
ny:d=vy:−vz,  nx:d=vx:−vzny=d⋅vy−vz,  nx=d⋅vx−vzn_y:d=v_y:-v_z,\ \ n_x:d=v_x:-v_z\\ n_y= \cfrac{d\sdot v_y}{-v_z}, \ \ n_x= \cfrac{d\sdot v_x}{-v_z}
따라서 초점거리와 뷰 좌표로부터 PndcP_{ndc}의 식은 다음과 같다.
Pndc=(nx,ny)=(d⋅vx−vz,d⋅vy−vz)=−d−vz(vx,vy)P_{ndc} = (n_x,n_y)=\left(\cfrac{d\sdot v_x}{-v_z},\cfrac{d\sdot v_y}{-v_z} \right)=-\cfrac{d}{-v_z}(v_x,v_y)
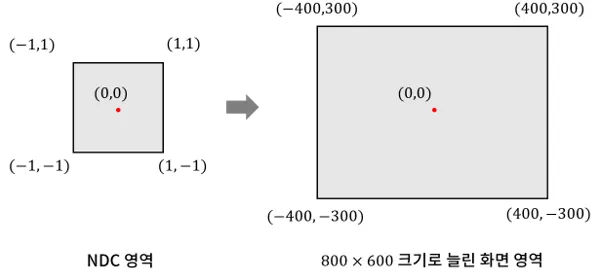
이제 NDC좌표를 계산했다면 모니터의 최종화면을 구성하자. NDC 좌표를 화면 해상도만큼 늘려주면 최종 스크린 좌표가 완성된다.
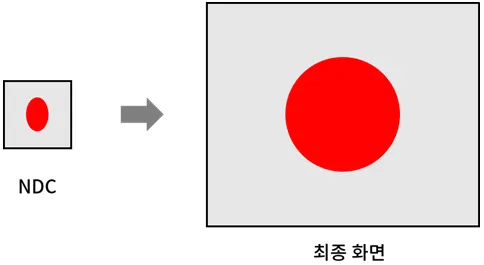
그런데 Free Aspect 방식으로 막 늘려버리면 물체가 찌그러지는 문제가 발생한다. 대부분의 경우 최종 화면이 1:1로 균등하지 않기 때문이다.
문제의 원인이 되는 화면의 가로와 세로의 비를 종횡비라고 한다. 이를 해결하기 위해 종횡비를 미리 파악해 NDC 단계에서 미리 찌그러뜨린 후에 펼치는 방법을 쓴다.
여기에서 사용한 종횡비는 세로를 기준으로 잡고 측정한 값이다. 800*600의 경우, 1.3333이된다.
Pndc=−dvz(vxa,vy)P_{ndc} = -\cfrac{d}{v_z}\left(\cfrac{v_x}{a}, v_y \right)
좌우로 찌그러트리려면 x축 값을 변경해야 하는데, 종횡비의 역수를 x축에 곱하면 다음과 같이 된다.
따라서 최종 행렬은 다음과 같다.
Pndc=P⋅v⃗=[1a⋅d−vz00d−vz]⋅[vxvy]P_{ndc} = P\sdot \vec v = \begin{bmatrix} \cfrac{1}{a}\sdot\cfrac{d}{-v_z} & 0\\ 0 & \cfrac{d}{-v_z} \end{bmatrix}\sdot \begin{bmatrix} v_x\\ v_y \end{bmatrix}
다만 한가지 짚고 넘어갈 점이 있다. 원근 투영행렬을 이렇게 생성하고 사용하려고 해도 변환할 점의 z값이 행렬에 사용되다 보니 변환할 점마다 항상 행렬을 새롭게 생성해야 해서 파이프라이닝 시 문제가 된다. z값을 쓰지 않고 카메라 설정만으로 행렬을 만들어보자.
우리가 유도한 투영 행렬은 분모가 모두 −vz-v_z를 분모로 한다는 점이다.
그럼 만약에 행렬에서 −vz-v_z를 제거하고 대신 결과에서 −vz-v_z를 나누어준다면?
그럼 NDC를 두 단계로 나눠보자.
P⋅v⃗=[da000d000−1]⋅[vxvyvz]=[da⋅vxd⋅vy−vz]P\sdot \vec v = \begin{bmatrix} \cfrac{d}{a} & 0 & 0\\ 0 & d & 0\\ 0 & 0 & -1 \end{bmatrix}\sdot \begin{bmatrix} v_x\\ v_y\\ v_z \end{bmatrix} =\begin{bmatrix} \cfrac{d}{a}\sdot v_x\\ d\sdot v_y\\ -v_z \end{bmatrix}
이렇게 생성된 벡터는 NDC좌표와는 다르지만 원근 투영 행렬 P는 점의 위치와 무관하게 카메라 설정 값으로만 구성이 가능하다. 이렇게 원근 투영행렬 P로 변환되는 좌표계를 클립 좌표계(Clip Coordinate)라고 부른다.
Pclip=(d⋅vxa,d⋅vy,−vz)P_{clip} = (\cfrac{d\sdot v_x}{a}, d\sdot v_y, -v_z)
클립좌표계에서 −vz-v_z를 나눠준다면 원하는 NDC를 찾을 수 있다.
이 투영행렬을 다른 행렬과의 곱을 위해 3 3사이즈에서 4 4 사이즈로 인위적으로 늘려준다. 빈 공간은 I로 메꿔준다.
P⋅v⃗=[da0000d0000−100001]⋅[vxvyvz1]=[da⋅vxd⋅vy−vz1]P\sdot \vec v = \begin{bmatrix} \cfrac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0 & 0 & -1 & 0\\ 0&0&0&1 \end{bmatrix}\sdot \begin{bmatrix} v_x\\ v_y\\ v_z\\ 1 \end{bmatrix} =\begin{bmatrix} \cfrac{d}{a}\sdot v_x\\ d\sdot v_y\\ -v_z\\ 1 \end{bmatrix}

Homogenous Coordinate Systems

NDC는 2차원 평면의 좌표계지만, 모든 점에 사용가능한 P를 제작하는 과정에서 차원이 한 단게 올라갔다.
이렇게 한 차원 높인 벡터를 사용하는 것을 보통 동차 좌표계(Homogenous Coordinate System)이라고 한다. Homogenous Coordinate와 Projection Space간의 연관성을 알아보자.
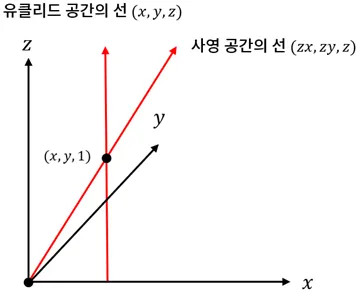
3차원의 사영 공간에서 평행하게 점을 이동시키면서 평면에 투영된 좌푯값이 어떻게 바뀌는지 관찰하자. 사영공간의 점과 투영된 점의 좌표는 카메라로부터 멀어질 수록 원점에 가까워지고, 카메라에 가까워질수록 커지는 반비례 관계를 가진다.
3차원 사영 공간의 점을(x′,y′,z′)(x',y',z')로 표기하고 해당 점이 투영된 NDC 좌표를 (x,y)(x,y)로 표기하자. NDC 좌푯값은 사영 공간의 마지막 차원 값 z′z'에 반비례로 영향을 받으므로 다음과 같은 관계가 성립한다.
x=x′z′,  y=y′z′x= \cfrac{x'}{z'},\ \ y=\cfrac{y'}{z'}
이번에는 NDC공간에서 직선의 방정식 y=ax+by = ax + b이 사실 사영 공간의 점들이 투영되어 만들어졌다고 생각해보자.
y=ax+by′z′=ax′z′+by′=ax′+bz′y = ax + b\\ \cfrac{y'}{z'} = a\cfrac{x'}{z'} + b\\ y' = ax'+bz'
이렇게 사영공간의 변수로 치환한 후 적절히 변수를 섞어주면 세 미지수의 차수가 모두 1차식으로 통일되는 신기한 현상이 일어난다.
이렇게 미지수에 대한 차수가 모두 동일한 방정식을 동차 방정식이라고 부르며, 이런 이유로 사영 공간이 사용하는 좌표계를 동차좌표계라고 부른다.

Depth

2차원 영역이었던 NDC 영역에 깊이 값을 추가하면 3차원 영역으로 NDC 영역이 확장된다. 이는 Depth 값을 측정하여 앞에 있는 놈이 앞에 그려지도록 하기 위함이다.
깊이 값은 동일하게 [-1,1]로 설정한다.
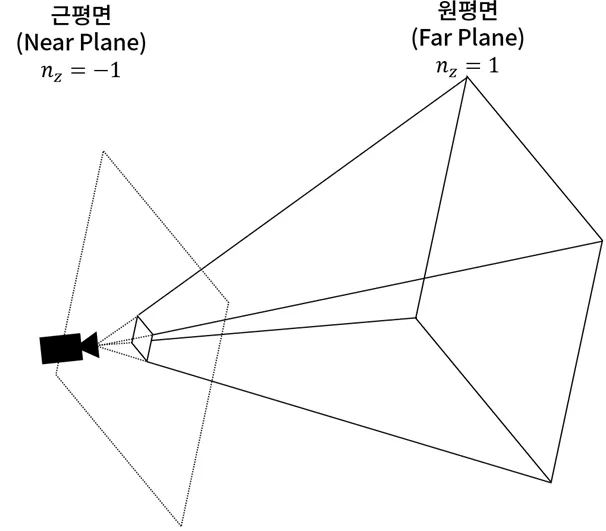
카메라에 부여한 시야각은 깊이와 무관하다. z값이 어느 비율 지점에 있는지 확인해줄 친구가 필요하며 따라서 우리는 카메라에 추가 속성을 부여해야한다. 이를 근평면(Near Plane)과 원평면(Far Plane)이라고 한다. 시야를 구성하는 사영 공간을 근평면과 원평면으로 잘라주면 아래와 같이 사각뿔에서 뾰족한 부분이 잘린 형태가 나오는데 이를 Frustum(절두체)라고 한다.
신기하게도 3차원 NDC 공간은 오른손 좌표계가 아닌 왼손 좌표계를 쓴다. 이는 Near이 -1이고, Far이 1이기 때문에 Z축이 안쪽으로 들어가는 방향으로 바뀌기 때문이다.
기존에 유도한 원근 투영 행렬을 가져오자.
P⋅v⃗=[da0000d0000−100001]⋅[vxvyvz1]=[da⋅vxd⋅vy−vz1]P\sdot \vec v = \begin{bmatrix} \cfrac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0 & 0 & -1 & 0\\ 0&0&0&1 \end{bmatrix}\sdot \begin{bmatrix} v_x\\ v_y\\ v_z\\ 1 \end{bmatrix} =\begin{bmatrix} \cfrac{d}{a}\sdot v_x\\ d\sdot v_y\\ -v_z\\ 1 \end{bmatrix}
다른 행렬과의 곱을 위해 기존의 행렬 사이즈를 억지로 늘렸는데 마지막 한 행을 깊이 계산을 위해 사용할 수 있도록 모든 행렬을 알차게 사용할 수 있게 되었다.
기존 행렬의 3행과 행을 교체하고, 3행은 깊이 값을 구하는 용도로 변경한다.
P⋅v⃗=[da0000d00ijkl00−10]⋅[vxvyvz1]=[da⋅vxd⋅vy?−vz]P\sdot \vec v = \begin{bmatrix} \cfrac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ \bf {\textcolor{red}i} & \bf {\textcolor{red}j} & \bf {\textcolor{red}k} & \bf {\textcolor{red}l}\\ 0 & 0 & -1 & 0 \end{bmatrix}\sdot \begin{bmatrix} v_x\\ v_y\\ v_z\\ 1 \end{bmatrix} =\begin{bmatrix} \cfrac{d}{a}\sdot v_x\\ d\sdot v_y\\ \bf {\textcolor{red}?}\\ -v_z \end{bmatrix}
Depth는 뷰 좌표계의 x축과 y축에 각각 직교하므로 아무 영향을 받지 않는다. 그러므로 앞의 두 요소와 i와 j값은 0으로 설정해야 한다.
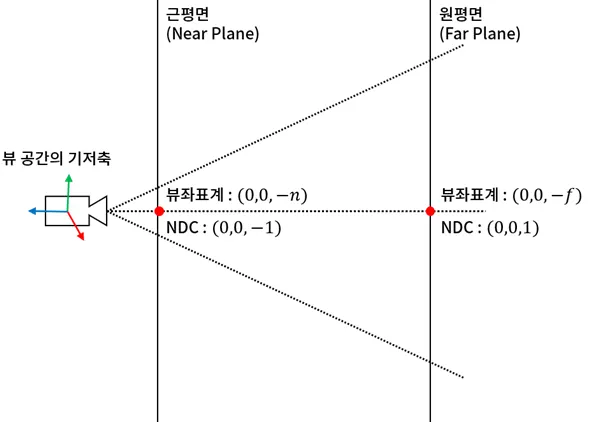
이제 k와 l을 구하기 위해 아까 설정한 근평면과 원평면을 사용할 것이다. 카메라로부터 근평면까지의 거리를 n, 원평면까지의 거리를 f라고 하자. 카메라로부터 n만큼 이동한 근평면 상에 위치한 점을 생각해보자. 이 점의 좌표는 0,0,-n,1이 될 것이다. 이는 깊이 값의 시작 지점이므로 NDC 좌표 (0,0,-1)에 대응된다. 마찬가지로 (0,0,-f,1)은 NDC(0,0,1)에 대응된다.
[da0000d0000kl00−10]⋅[00−n1]=[00?n] \begin{bmatrix} \cfrac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0&0& k & l\\ 0 & 0 & -1 & 0 \end{bmatrix}\sdot \begin{bmatrix} 0\\ 0\\ -n\\ 1 \end{bmatrix} =\begin{bmatrix} 0\\ 0\\ ?\\ \bf {\textcolor{red}n}\\ \end{bmatrix}
[da0000d0000kl00−10]⋅[00−f1]=[00?f] \begin{bmatrix} \cfrac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0&0& k & l\\ 0 & 0 & -1 & 0 \end{bmatrix}\sdot \begin{bmatrix} 0\\ 0\\ -f\\ 1 \end{bmatrix} =\begin{bmatrix} 0\\ 0\\ ?\\ \bf {\textcolor{red}f}\\ \end{bmatrix}
아직 k와 l의 값을 특정할 수 없으므로 클립 좌표의 세번째 요소를 계산할 수 없다.
하지만 클립 좌표의 네번째 요소로 나머지 세 값을 나눠 NDC좌표를 계산하고 NDC 좌표의 값은 각각 -1와 1임을 알고 있다.
따라서 근평면의 클립 좌표는 각각 (0,0,−n,n)(0,0,-n,n),(0,0,f,f)(0,0,f,f)가 되어야 함을 알 수 있다.
[da0000d0000kl00−10]⋅[00−n1]=[00−nn] \begin{bmatrix} \cfrac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0&0& k & l\\ 0 & 0 & -1 & 0 \end{bmatrix}\sdot \begin{bmatrix} 0\\ 0\\ -n\\ 1 \end{bmatrix} =\begin{bmatrix} 0\\ 0\\ \bf {\textcolor{red}{-n}}\\ n\\ \end{bmatrix}
[da0000d0000kl00−10]⋅[00−f1]=[00ff] \begin{bmatrix} \cfrac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0&0& k & l\\ 0 & 0 & -1 & 0 \end{bmatrix}\sdot \begin{bmatrix} 0\\ 0\\ -f\\ 1 \end{bmatrix} =\begin{bmatrix} 0\\ 0\\ \bf {\textcolor{red}f}\\ f\\ \end{bmatrix}
오… 연립방정식 타임.
−kn+l=−n−kf+l=f-kn+l=-n\\ -kf+l=f
k=n+fn−f,   l=2nfn−fk = \cfrac{n+f}{n-f},\ \ \ l = \cfrac{2nf}{n-f}
이로써 최종 원근 투영 행렬의 퍼즐 조각을 맞췄다!!!! 깊이 값까지 산출해주는 최종 원근 투영 행렬 P는 다음과 같다.
[da0000d0000n+fn−f2nfn−f00−10] \begin{bmatrix} \cfrac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0&0& \cfrac{n+f}{n-f} & \cfrac{2nf}{n-f}\\ 0 & 0 & -1 & 0 \end{bmatrix}
Next chapter