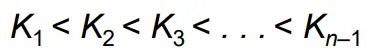Previous chapter
Storage Access
byte-addressable : 바이트 단위로 데이터를 읽어들인다. (메모리, 캐시 등)
block-addressable : 페이지, 블록 단위로 데이터를 읽어들인다. (플래시 메모리 밑의 레벨)
data transfer의 빈도를 줄이는 것이 메인 목표. → 오버헤드가 높기 때문!
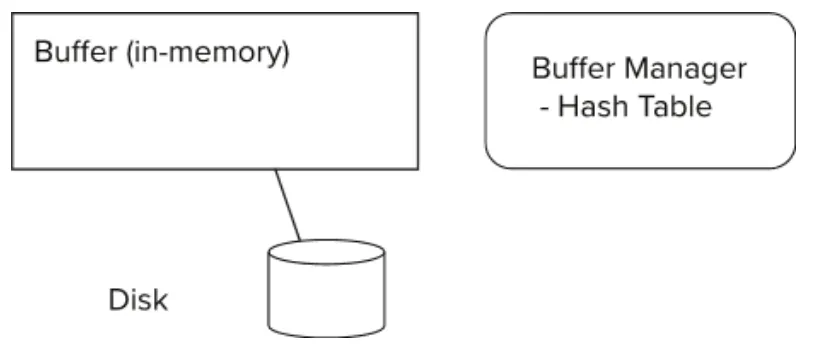
Buffer : 메인 메모리에 디스크 블록을 저장하는 부분
Buffer Manager : 메인 메모리에 버퍼 공간을 할당시키는 서브시스템, 또는 관리주체
Buffer Manager
버퍼 매니저는 디스크에 있는 데이터를 읽을 때, 미리 메모리에 올라와있다면 바로 리턴, 아니면 읽는 구조.
•
블록이 버퍼에 없을 경우
◦
블록을 버퍼 스페이스에 할당한다.
▪
필요에 따라서는 정책에 의해서 희생될 블록과 해당 블록을 교체한다.
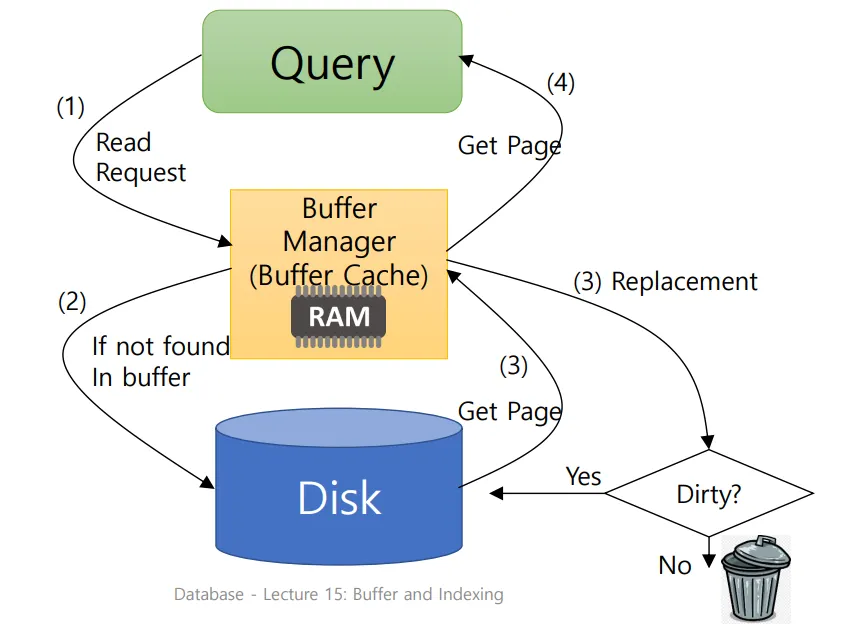
Read
Read Request가 발생할 때 버퍼 매니저에서 블록을 탐색한다.
블록이 버퍼에 없을 경우
디스크에서 해당 블록을 버퍼에 들고온다.
만약 버퍼가 가득찰 경우, 교체정책에 의해 이전 블록과 교체한다.
버퍼에 있는 데이터가 수정되었을 경우(Dirty) 디스크에 다시 쓴다.
이후 버퍼에서 다시 탐색을 진행해 블록을 들고온다.
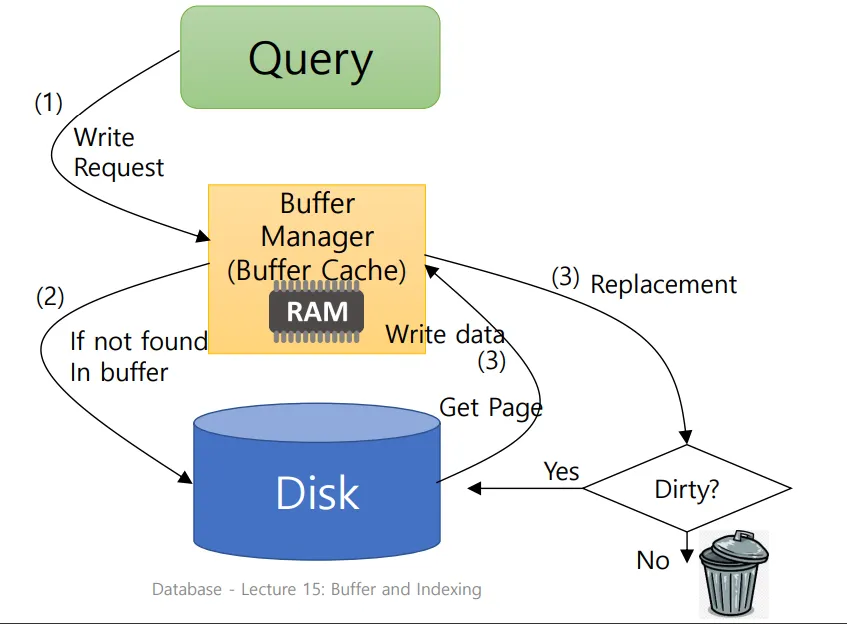
Write
쓰기 리퀘스트
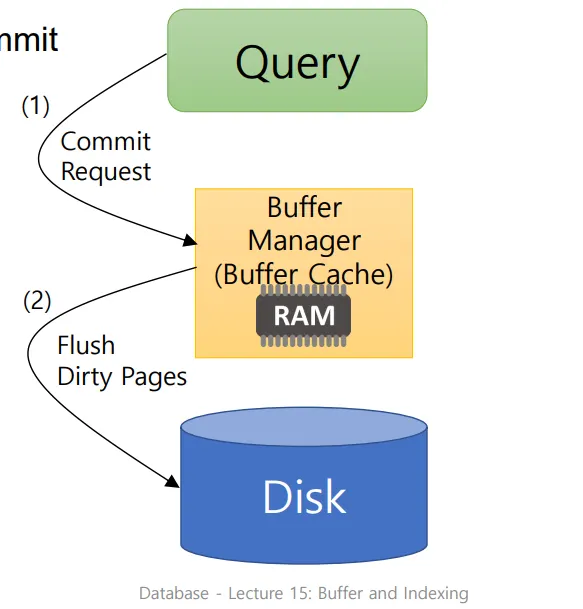
Transaction
Buffer-Replacement strategy
데이터베이스를 읽거나 고치고 있는 경우, 현재 데이터베이스가 누군가에 의해 사용중임을 나타내는
•
Pinned Block :
◦
Pin :
◦
Unpin :
mutex 짭?
•
Shared and exclusive locks on buffer
◦
Shared lock : 읽기만 하는 스레드는 여러개가 접근해도 DB 페이지를 고치지 않기 때문에 여러 스레드가 읽기가 가능하다.
◦
Exclusive lock : 한 스레드가 데이터의 수정을 진행할때, 다른 모든 스레드는 읽기와 쓰기 모두 불가능한 상태로 변경된다.
대부분의 OS는 LRU 기반 정책을 사용한다.
그러나 데이터베이스는 연산의 특성(join등) 때문에 LRU가 반드시 좋다고 할 수 없다!
•
Toss-immediate Strategy
◦
특정 데이터베이스 페이지가 연산이 다 끝날 경우, 일단 flush를 진행한다.
•
Most recently used strategy
◦
특정
데이터 연산은
Indexing
대용량 데이터가 있을때 데이터를 빠르게 찾아서 사용하는 법이다.
•
Search Key : 테이블을 생성할 때 기반(인덱스로 활용됨!)이 된 키
•
인덱스 파일은 Search-key 와 pointer의 묶음으로 사용된다.
•
인덱스는 실제 데이터를 가지고 있지 않으며 테이블보다 사이즈가 작다.
◦
Ordered Indices : 키들이 순서대로 저장된다.
◦
Hash indices : ??????????????????????????????????????????????????????????????????
두개는 분명하게 차이가 있으며 특징이 다름.
Index Evaluation matrices
point query : 쿼리가 단 하나의 데이터를 원하는 경우 (key = value)
Range Query : 쿼리가 복수의 데이터를 원하는 경우 (low<key<high)
Access time : 데이터를 찾을 때 얼마나 시간이 걸리는가?
Insertion time : 데이터를 삽입할 때 얼마나 시간이 걸리는가?
Deletion time : 데이터를 삭제할 때 얼마나 시간이 걸리는가?
Space overhead : ?
Order Indices
search key에 의해 정렬된 상태
•
Clustered index(primary index)
◦
프라이머리 키로 만든 인덱스
•
Secondary index(nonclustered index)
◦
다른 attribute(그러나 빈번하게 사용되는)로 인덱스를 빌딩하는 것!
•
Index
Dense Index Files
밀집한 인덱스 모든 데이터베이스의 튜플과 매칭이 되는 경우를 말한다.(primary index의 경우 여기에 해당)
Sparse Index Files
몇몇 키만 들어가있는 인덱스 파일. → 인덱스의
Multilevel Index
인덱스가 메모리보다 크면 Storage access가 발생하기 때문에 코스트가 높아지게 된다.
B+ Tree Index
B+트리는 다음 특성을 모두 만족하는 트리이다.
•
Root → Leaf까지의 모든 length가 같은 Balanced tree이다.
•
leaf노드는 (n-1)/2와 n-1개 사이의 개수를 가지고 있다.
•
스페셜 케이스
◦
루트 노드가 리프 노드가 아닐 경우, 2개의 child를 가지고 있어야 한다.???
B+트리는 데이터의 삽입과 삭제에도 불구하고 일정한 성능을 계속 유지하기 때문에 널리 쓰인다.
다만, B+트리가 장점만 있는 것은 아니다. 구조 상 노드 안에 데이터가 최소로 있을 때 공간이 반 정도 비는 현상이 발생하므로, 낭비되는 공간이 발생한다.
B+ Node Structure
•
P(n) : 포인터
•
K(n) : 키
search key는 오름차순으로 정렬된다. (일단 duplicates는 없다는 가정하에)
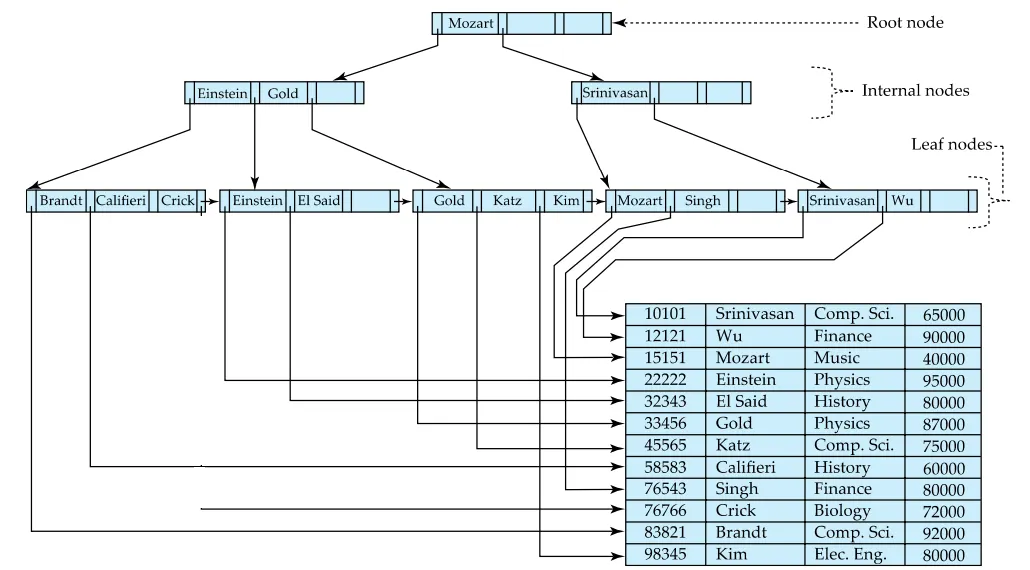
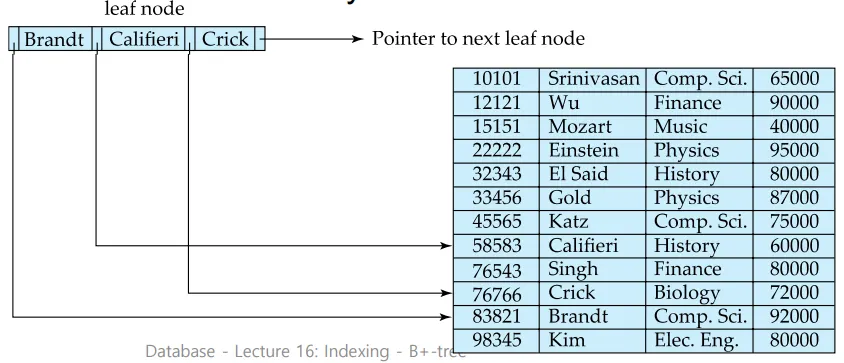
Leaf Node in B+-Tree
Leaf노드에 저장된 데이터는 반드시 오름차순으로 정렬된다.
P(n) = next leaf node로의 포인터, 이를 sibling pointer이라고 한다.
형제 노드와 비교했을 때 왼쪽에 있는 최대값은 오른쪽에 있는 최소값보다 값이 작아야 한다.
각 리프 노드는 n-1개의 키 값을 가질 수 있는데, 이 리프 노드는 적어도 (n-1)/2개의 값을 포함해야한다.
Non-Leaf Node in B+-Tree
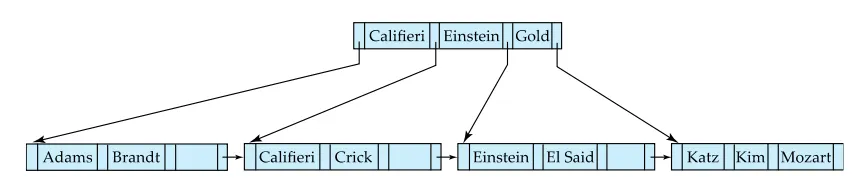
Examples
Observation about B+-Tree
•
리프노드가 아닌 레벨은 sparse한 인덱스 구조를 가지게 된다.
•
검색 코스트가 트리의 높이이므로, 생각보다 트리의 높이가 크지 않게 설계된다.
Queries on B+-Tree
function find(v)
C = root
while(c is not a leaf node)
Let i be least number s.t. V<=K(i)
if(there is no such number i)
C
복사
Range Queries : 최소값 최대값을 줘서 그 사이의 값을 찾는 것 → 보통 linear search + linked list
보통은 노드는 4kb기반으로 최적화되어있음 n은 기본적으로 100정도..?
Non Unique keys
composite키를 찾아서 u
Updates on B+-Trees
Insertion
•
record가 파일에 이미 추가된 상태라고 가정하자.
◦
prt을 record의 포인터
◦
Deletion
Redistribution of Sibling Nodes
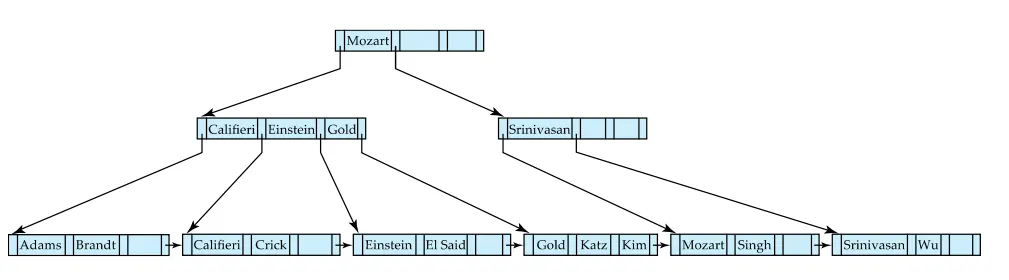
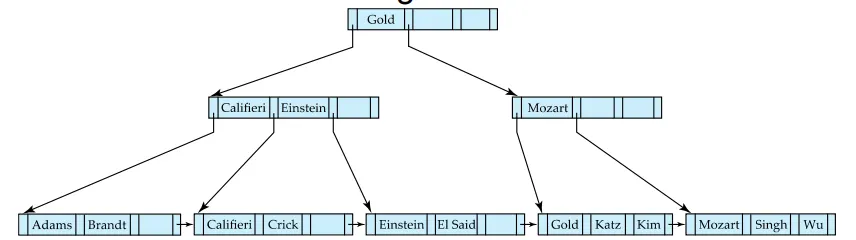
Singh와 Wu를 삭제한 후의 B+-트리
과정
•
Singh또는 Wu만 삭제했을 때는 데이터가 n/2 이하로 떨어지지 않았으므로 트리는 그대로 유지된다.
•
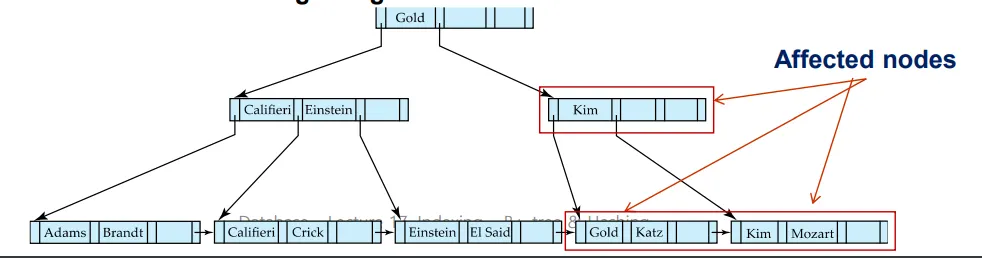
Singh과 Wu 모두 삭제되었을 때, 데이터가 n/2보다 작으므로, Merge연산을 진행한다.
◦
Mozart는 Gold의 노드에 포함되게 된다.
◦
그러나 노드의 수용개수가 초과되어 다시 Split을 진행한다.
•
Gold Katz Kim Mozart는 Gold Katz \ Kim Mozart로 스플릿된다.
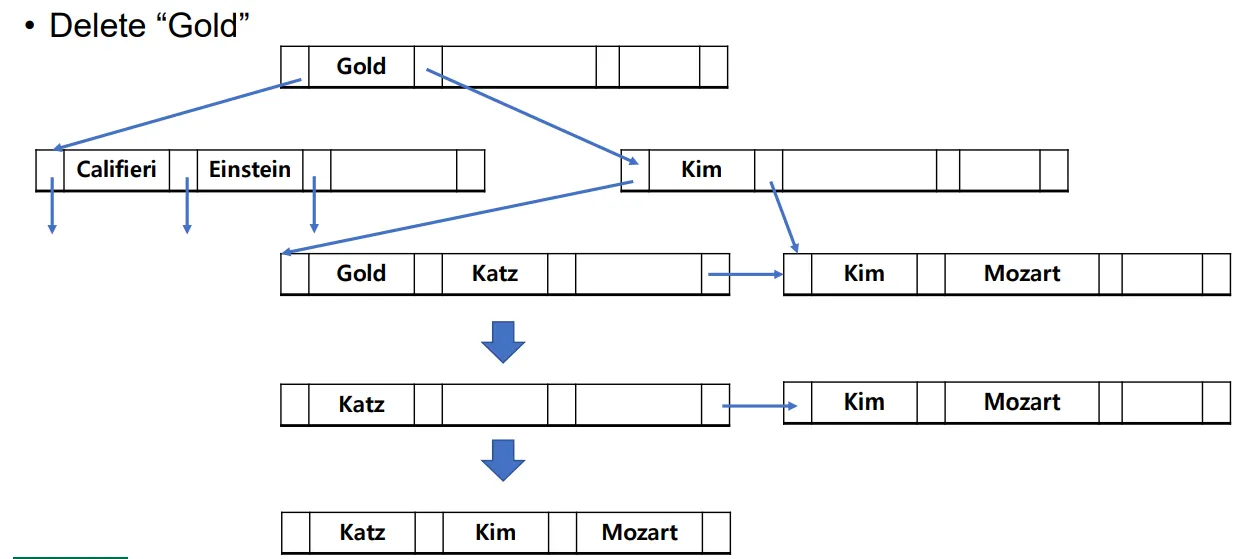
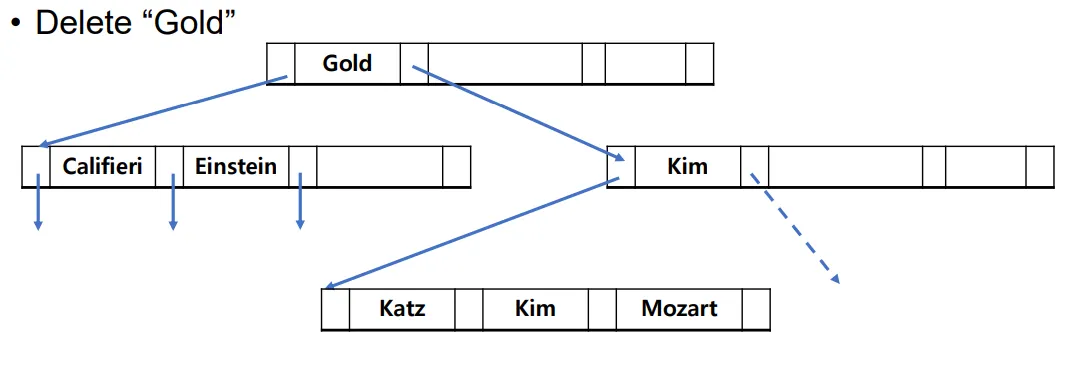
Gold 삭제
Updates on Deletion
(K, Ptr)에 있는 데이터를 삭제
Complexity of Updates
시간복잡도
insert와 delete는 엔트리의 최대 fanout이 n일 때 최대 O()까지 걸릴 수 있다.
실무에서는 스플릿과 머지가 생각보다 잘 일어나지 않으며, leaf노드에만 영향을 미친다고 생각하면 편하다.
노드의 평균 점유율은 insertion 순서에 ????
B+-Tree File Organization
Indexing Strings
fanout이 가변이다!!!
엔트리의 개수가 더이상 중요하지 않으며, 엔트리의 공간이 많더라도 하나일 수 있다.
Bulk Loading and Buttom-Up Build
B-Tree Index File
Other Issues on Indexing
Next chapter